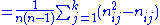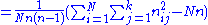Fleiss' kappa
Encyclopedia
Fleiss' kappa is a statistical measure for assessing the reliability of agreement
between a fixed number of raters when assigning categorical ratings to a number of items or classifying items. This contrasts with other kappas such as Cohen's kappa
, which only work when assessing the agreement between two raters. The measure calculates the degree of agreement in classification over that which would be expected by chance and is scored as a number between 0 and 1. There is no generally agreed on measure of significance, although guidelines have been given.
Fleiss' kappa can be used only with binary or nominal-scale ratings. No version is available for ordered-categorical ratings.
statistic, a statistical measure of inter-rater reliability
. It is also related to Cohen's kappa
statistic. Whereas Scott's pi and Cohen's kappa work for only two raters, Fleiss' kappa works for any number of raters giving categorical ratings (see nominal data), to a fixed number of items. It can be interpreted as expressing the extent to which the observed amount of agreement among raters exceeds what would be expected if all raters made their ratings completely randomly. It is important to note that whereas Cohen's kappa assumes the same two raters have rated a set of items, Fleiss' kappa specifically assumes that although there are a fixed number of raters (e.g., three), different items are rated by different individuals (Fleiss, 1971, p.378). That is, Item 1 is rated by Raters A, B, and C; but Item 2 could be rated by Raters D, E, and F.
Agreement can be thought of as follows, if a fixed number of people assign numerical ratings to a number of items then the kappa will give a measure for how consistent the ratings are. The kappa, , can be defined as,
, can be defined as,
(1)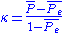
The factor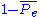 gives the degree of agreement that is attainable above chance, and,
gives the degree of agreement that is attainable above chance, and, 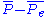 gives the degree of agreement actually achieved above chance. If the raters are in complete agreement then
gives the degree of agreement actually achieved above chance. If the raters are in complete agreement then  . If there is no agreement among the raters (other than what would be expected by chance) then
. If there is no agreement among the raters (other than what would be expected by chance) then  .
.
An example of the use of Fleiss' kappa may be the following: Consider fourteen psychiatrists are asked to look at ten patients. Each psychiatrist gives one of possibly five diagnoses to each patient. The Fleiss' kappa can be computed from this matrix (see example below) to show the degree of agreement between the psychiatrists above the level of agreement expected by chance.
First calculate pj, the proportion of all assignments which were to the j-th category:
(2)
Now calculate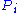 , the extent to which raters agree for the i-th subject (i.e., compute how many rater--rater pairs are in agreement, relative to the number of all possible rater--rater pairs):
, the extent to which raters agree for the i-th subject (i.e., compute how many rater--rater pairs are in agreement, relative to the number of all possible rater--rater pairs):
(3)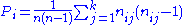
Now compute , the mean of the
, the mean of the 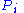 's, and
's, and  which go into the formula for
which go into the formula for  :
:
(4)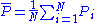
(5)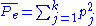
 ) assign ten "subjects" (
) assign ten "subjects" (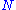 ) to a total of five categories (
) to a total of five categories (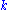 ). The categories are presented in the columns, while the subjects are presented in the rows. Each cell is filled with the number of raters who agreed that a certain subject belongs to a certain category.
). The categories are presented in the columns, while the subjects are presented in the rows. Each cell is filled with the number of raters who agreed that a certain subject belongs to a certain category.
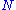 = 10,
= 10,  = 14,
= 14, 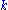 = 5
= 5
Sum of all cells = 140
Sum of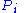 = 3.780
= 3.780
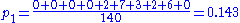
And taking the second row,

In order to calculate , we need to know the sum of
, we need to know the sum of 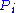 ,
,
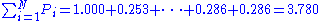
Over the whole sheet,
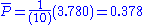
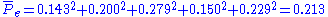
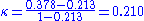
 values. This table is however by no means universally accepted; They supplied no evidence to support it, basing it instead on personal opinion. It has been noted that these guidelines may be more harmful than helpful, as the number of categories and subjects will affect the magnitude of the value. The kappa will be higher when there are fewer categories.
values. This table is however by no means universally accepted; They supplied no evidence to support it, basing it instead on personal opinion. It has been noted that these guidelines may be more harmful than helpful, as the number of categories and subjects will affect the magnitude of the value. The kappa will be higher when there are fewer categories.
Inter-rater reliability
In statistics, inter-rater reliability, inter-rater agreement, or concordance is the degree of agreement among raters. It gives a score of how much homogeneity, or consensus, there is in the ratings given by judges. It is useful in refining the tools given to human judges, for example by...
between a fixed number of raters when assigning categorical ratings to a number of items or classifying items. This contrasts with other kappas such as Cohen's kappa
Cohen's kappa
Cohen's kappa coefficient is a statistical measure of inter-rater agreement or inter-annotator agreement for qualitative items. It is generally thought to be a more robust measure than simple percent agreement calculation since κ takes into account the agreement occurring by chance. Some...
, which only work when assessing the agreement between two raters. The measure calculates the degree of agreement in classification over that which would be expected by chance and is scored as a number between 0 and 1. There is no generally agreed on measure of significance, although guidelines have been given.
Fleiss' kappa can be used only with binary or nominal-scale ratings. No version is available for ordered-categorical ratings.
Introduction
Fleiss' kappa is a generalisation of Scott's piScott's Pi
Scott's pi is a statistic for measuring inter-rater reliability for nominal data in communication studies. Textual entities are annotated with categories by different annotators, and various measures are used to assess the extent of agreement between the annotators, one of which is Scott's pi...
statistic, a statistical measure of inter-rater reliability
Inter-rater reliability
In statistics, inter-rater reliability, inter-rater agreement, or concordance is the degree of agreement among raters. It gives a score of how much homogeneity, or consensus, there is in the ratings given by judges. It is useful in refining the tools given to human judges, for example by...
. It is also related to Cohen's kappa
Cohen's kappa
Cohen's kappa coefficient is a statistical measure of inter-rater agreement or inter-annotator agreement for qualitative items. It is generally thought to be a more robust measure than simple percent agreement calculation since κ takes into account the agreement occurring by chance. Some...
statistic. Whereas Scott's pi and Cohen's kappa work for only two raters, Fleiss' kappa works for any number of raters giving categorical ratings (see nominal data), to a fixed number of items. It can be interpreted as expressing the extent to which the observed amount of agreement among raters exceeds what would be expected if all raters made their ratings completely randomly. It is important to note that whereas Cohen's kappa assumes the same two raters have rated a set of items, Fleiss' kappa specifically assumes that although there are a fixed number of raters (e.g., three), different items are rated by different individuals (Fleiss, 1971, p.378). That is, Item 1 is rated by Raters A, B, and C; but Item 2 could be rated by Raters D, E, and F.
Agreement can be thought of as follows, if a fixed number of people assign numerical ratings to a number of items then the kappa will give a measure for how consistent the ratings are. The kappa,
 , can be defined as,
, can be defined as,(1)
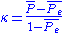
The factor
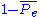 gives the degree of agreement that is attainable above chance, and,
gives the degree of agreement that is attainable above chance, and, 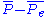 gives the degree of agreement actually achieved above chance. If the raters are in complete agreement then
gives the degree of agreement actually achieved above chance. If the raters are in complete agreement then  . If there is no agreement among the raters (other than what would be expected by chance) then
. If there is no agreement among the raters (other than what would be expected by chance) then  .
.An example of the use of Fleiss' kappa may be the following: Consider fourteen psychiatrists are asked to look at ten patients. Each psychiatrist gives one of possibly five diagnoses to each patient. The Fleiss' kappa can be computed from this matrix (see example below) to show the degree of agreement between the psychiatrists above the level of agreement expected by chance.
Equations
Let N be the total number of subjects, let n be the number of ratings per subject, and let k be the number of categories into which assignments are made. The subjects are indexed by i = 1, ... N and the categories are indexed by j = 1, ... k. Let nij represent the number of raters who assigned the i-th subject to the j-th category.First calculate pj, the proportion of all assignments which were to the j-th category:
(2)

Now calculate
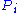 , the extent to which raters agree for the i-th subject (i.e., compute how many rater--rater pairs are in agreement, relative to the number of all possible rater--rater pairs):
, the extent to which raters agree for the i-th subject (i.e., compute how many rater--rater pairs are in agreement, relative to the number of all possible rater--rater pairs):(3)
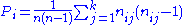
Now compute
 , the mean of the
, the mean of the 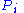 's, and
's, and  which go into the formula for
which go into the formula for  :
:(4)
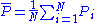
(5)
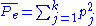
Worked example
In the following example, fourteen raters ( ) assign ten "subjects" (
) assign ten "subjects" (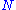 ) to a total of five categories (
) to a total of five categories (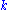 ). The categories are presented in the columns, while the subjects are presented in the rows. Each cell is filled with the number of raters who agreed that a certain subject belongs to a certain category.
). The categories are presented in the columns, while the subjects are presented in the rows. Each cell is filled with the number of raters who agreed that a certain subject belongs to a certain category.Data
See table to the right.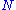 = 10,
= 10,  = 14,
= 14, 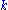 = 5
= 5Sum of all cells = 140
Sum of
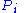 = 3.780
= 3.780Calculations
For example, taking the first column,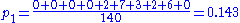
And taking the second row,

In order to calculate
 , we need to know the sum of
, we need to know the sum of 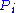 ,
,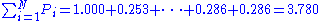
Over the whole sheet,
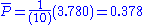
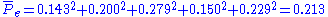
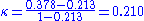
Significance
Landis and Koch (1977) gave the following table for interpreting values. This table is however by no means universally accepted; They supplied no evidence to support it, basing it instead on personal opinion. It has been noted that these guidelines may be more harmful than helpful, as the number of categories and subjects will affect the magnitude of the value. The kappa will be higher when there are fewer categories.
values. This table is however by no means universally accepted; They supplied no evidence to support it, basing it instead on personal opinion. It has been noted that these guidelines may be more harmful than helpful, as the number of categories and subjects will affect the magnitude of the value. The kappa will be higher when there are fewer categories.  | Interpretation |
|---|---|
| < 0 | Poor agreement |
| 0.01 – 0.20 | Slight agreement |
| 0.21 – 0.40 | Fair agreement |
| 0.41 – 0.60 | Moderate agreement |
| 0.61 – 0.80 | Substantial agreement |
| 0.81 – 1.00 | Almost perfect agreement |
See also
- Cohen's kappaCohen's kappaCohen's kappa coefficient is a statistical measure of inter-rater agreement or inter-annotator agreement for qualitative items. It is generally thought to be a more robust measure than simple percent agreement calculation since κ takes into account the agreement occurring by chance. Some...
- Pearson product-moment correlation coefficientPearson product-moment correlation coefficientIn statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
Further reading
- Fleiss, J. L. and Cohen, J. (1973) "The equivalence of weighted kappa and the intraclass correlation coefficient as measures of reliability" in Educational and Psychological Measurement, Vol. 33 pp. 613–619
- Fleiss, J. L. (1981) Statistical methods for rates and proportions. 2nd ed. (New York: John Wiley) pp. 38–46
- Gwet, K. L. (2008) "Computing inter-rater reliability and its variance in the presence of high agreement", British Journal of Mathematical and Statistical Psychology, Vol. 61, pp29–48
External links
- Kappa: Pros and Cons contains a good bibliography of articles about the coefficient.
- Online Kappa Calculator calculates a variation of Fleiss' kappa.
- AgreeStat a Point-And-Click Excel2007 VBA Program calculates various inter-rater reliability coefficients and associated variances.