The firing squad synchronization problem is a problem in computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

 and cellular automata

Cellular automaton

A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...

 in which the goal is to design a cellular automaton

Cellular automaton

A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...

 that, starting with a single active cell, eventually reaches a state in which all cells are simultaneously active. It was first proposed by John Myhill

John Myhill

John R. Myhill was a mathematician, born in 1923. He received his Ph.D. from Harvard University under Willard Van Orman Quine in 1949. He was professor at SUNY Buffalo from 1966 until his death in 1987...

 in 1957 and published (with a solution) in 1962 by Edward Moore

Edward F. Moore

Edward Forrest Moore was an American professor of mathematics and computer science, the inventor of the Moore finite state machine, and an early pioneer of artificial life....

.

Problem statement

The name of the problem comes from an analogy with real-world firing squads: the goal is to design a system of rules according to which a general can command a squad of troops to fire, and cause them to all fire their guns simultaneously.

More formally, the problem concerns cellular automata, arrays of finite state machines called "cells" arranged in a line, such that at each time step each machine transitions to a new state as a function of its previous state and the states of its two neighbors in the line. For the firing squad problem, the line consists of a finite number of cells, and the rule according to which each machine transitions to the next state should be the same for all of the cells interior to the line, but the transition functions of the two endpoints of the line are allowed to differ, as these two cells are each missing a neighbor on one of their two sides.

The states of each cell include three distinguished states: "active", "quiescent", and "firing", and the transition function must be such that a cell that is quiescent and whose neighbors are quiescent remains quiescent. Initially, at time , all states are quiescent except for the cell at the far left (the general), which is active. The goal is to design a set of states and a transition function such that, no matter how long the line of cells is, there exists a time such that every cell transitions to the firing state at time , and such that no cell belongs to the firing state prior to time .

Solutions

The first solution to the FSSP was found by John McCarthy

John McCarthy (computer scientist)

John McCarthy was an American computer scientist and cognitive scientist. He coined the term "artificial intelligence" , invented the Lisp programming language and was highly influential in the early development of AI.McCarthy also influenced other areas of computing such as time sharing systems...

 and Marvin Minsky

Marvin Minsky

Marvin Lee Minsky is an American cognitive scientist in the field of artificial intelligence , co-founder of Massachusetts Institute of Technology's AI laboratory, and author of several texts on AI and philosophy.-Biography:...

 and was published in Sequential Machines by Moore

Edward F. Moore

Edward Forrest Moore was an American professor of mathematics and computer science, the inventor of the Moore finite state machine, and an early pioneer of artificial life....

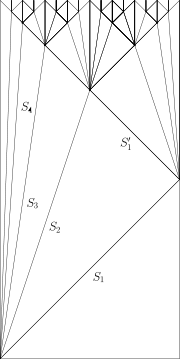
. Their solution involves propagating two waves down the line of soldiers: a fast wave and a slow wave moving three times as slow. The fast wave bounces off the other end of the line and meets the slow wave in the centre. The two waves then split into four waves, a fast and slow wave moving in either direction from the centre, effectively splitting the line into two equal parts. This process continues, subdividing the line until each division is of length 1. At this moment, every soldier fires. This solution requires 3n units of time for n soldiers.

A solution using a minimal amount of time was later found by ; his solution used thousands of states, but required only units of time for soldiers. A solution using a smaller amount of time cannot exist. improved this solution, using the same amount of time but only 16 states. further improved it to eight states, and proved that no four-state solution exists; Peter Sanders later found that Balzer's search procedure was incomplete, but managed to reaffirm the four-state non-existence result through a corrected search procedure. Finally, the best currently known solution, a minimal-time solution using six states, was introduced by . It is still unknown whether a five-state solution exists.

In the minimal-time solutions, the general sends to the right signals at speeds . The signal reflects at the right end of the line, and meets signal (for ) at cell . When reflects, it also creates a new general at the right end. Signals are constructed using auxiliary signals, which propagate to the left. Every second time a signal moves (to the right), it sends an auxiliary signal to the left. moves on its own at speed 1 while each of the slower signals moves only when it gets an auxiliary signal.

Generalizations

The firing squad synchronization problem has been generalized to many other types of cellular automaton, including higher dimensional arrays of cells . Variants of the problem with different initial conditions have also been considered .

Solutions to the firing squad problem may also be adapted to other problems. For instance, designed a cellular automaton algorithm to generate the prime number

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

s based on an earlier solution to the firing squad synchronization problem.