
Filling radius
Encyclopedia
In Riemannian geometry
, the filling radius of a Riemannian manifold
X is a metric invariant of X. It was originally introduced in 1983 by Mikhail Gromov, who used it to prove his systolic inequality for essential manifolds
, vastly generalizing Loewner's torus inequality
and Pu's inequality for the real projective plane, and creating Systolic geometry in its modern form.
The filling radius of a simple loop C in the plane is defined as the largest radius, R>0, of a circle that fits inside C:
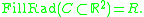
 -neighborhoods of the loop C, denoted
-neighborhoods of the loop C, denoted
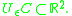
As increases, the
increases, the  -neighborhood
-neighborhood  swallows up more and more of the interior of the loop. The last point to be swallowed up is precisely the center of a largest inscribed circle. Therefore we can reformulate the above definition by defining
swallows up more and more of the interior of the loop. The last point to be swallowed up is precisely the center of a largest inscribed circle. Therefore we can reformulate the above definition by defining
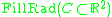 to be the infimum of
to be the infimum of  such that the loop C contracts to a point in
such that the loop C contracts to a point in  .
.
Given a compact manifold X imbedded in, say, Euclidean space E, we could define the filling radius relative to the imbedding, by minimizing the size of the neighborhood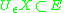 in which X could be homotoped to something smaller dimensional, e.g., to a lower dimensional polyhedron. Technically it is more convenient to work with a homological definition.
in which X could be homotoped to something smaller dimensional, e.g., to a lower dimensional polyhedron. Technically it is more convenient to work with a homological definition.
 or
or 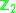 , depending on whether or not X is orientable. Then the fundamental class
, depending on whether or not X is orientable. Then the fundamental class
, denoted [X], of a compact n-dimensional manifold X, is a generator of the homology group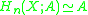 , and we set
, and we set
where is the inclusion homomorphism.
is the inclusion homomorphism.
To define an absolute filling radius in a situation where X is equipped with a Riemannian metric g, Gromov proceeds as follows. One exploits an imbedding due to Kazimierz Kuratowski
(the first name is sometimes spelled with a "C"). One imbeds X in the Banach space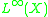 of bounded Borel functions on X, equipped with the sup norm . Namely, we map a point
of bounded Borel functions on X, equipped with the sup norm . Namely, we map a point 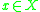 to the function
to the function  defined by the formula
defined by the formula 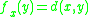
for all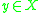 , where d is the distance function defined by the metric. By the triangle inequality we have
, where d is the distance function defined by the metric. By the triangle inequality we have 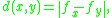 and therefore the imbedding is strongly isometric, in the precise sense that internal distance and ambient distance coincide. Such a strongly isometric imbedding is impossible if the ambient space is a Hilbert space, even when X is the Riemannian circle (the distance between opposite points must be
and therefore the imbedding is strongly isometric, in the precise sense that internal distance and ambient distance coincide. Such a strongly isometric imbedding is impossible if the ambient space is a Hilbert space, even when X is the Riemannian circle (the distance between opposite points must be
π, not 2!). We then set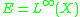 in the formula above, and define
in the formula above, and define

with a metric of constant curvature is a third of its Riemannian diameter, see (Katz, 1983). Equivalently, the filling radius is a sixth of the systole in these cases. The precise value is also known for the n-spheres (Katz, 1983).
The filling radius is linearly related to the systole of an essential manifold
M. Namely, the systole of such an M is at most six times its filling radius, see (Gromov, 1983). The inequality is optimal in the sense that the boundary case of equality is attained by the real projective spaces as above.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the filling radius of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
X is a metric invariant of X. It was originally introduced in 1983 by Mikhail Gromov, who used it to prove his systolic inequality for essential manifolds
Gromov's systolic inequality for essential manifolds
In the mathematical field of Riemannian geometry, M. Gromov's systolic inequality bounds the length of the shortest non-contractible loop on a Riemannian manifold in terms of the volume of the manifold...
, vastly generalizing Loewner's torus inequality
Loewner's torus inequality
In differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus.-Statement:...
and Pu's inequality for the real projective plane, and creating Systolic geometry in its modern form.
The filling radius of a simple loop C in the plane is defined as the largest radius, R>0, of a circle that fits inside C:
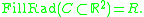
Dual definition via neighborhoods
There is a kind of a dual point of view that allows one to generalize this notion in an extremely fruitful way, as shown by Gromov. Namely, we consider the -neighborhoods of the loop C, denoted
-neighborhoods of the loop C, denoted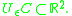
As
 increases, the
increases, the  -neighborhood
-neighborhood  swallows up more and more of the interior of the loop. The last point to be swallowed up is precisely the center of a largest inscribed circle. Therefore we can reformulate the above definition by defining
swallows up more and more of the interior of the loop. The last point to be swallowed up is precisely the center of a largest inscribed circle. Therefore we can reformulate the above definition by defining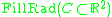 to be the infimum of
to be the infimum of  such that the loop C contracts to a point in
such that the loop C contracts to a point in  .
.Given a compact manifold X imbedded in, say, Euclidean space E, we could define the filling radius relative to the imbedding, by minimizing the size of the neighborhood
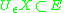 in which X could be homotoped to something smaller dimensional, e.g., to a lower dimensional polyhedron. Technically it is more convenient to work with a homological definition.
in which X could be homotoped to something smaller dimensional, e.g., to a lower dimensional polyhedron. Technically it is more convenient to work with a homological definition.Homological definition
Denote by A the coefficient ring or
or 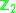 , depending on whether or not X is orientable. Then the fundamental class
, depending on whether or not X is orientable. Then the fundamental classFundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
, denoted [X], of a compact n-dimensional manifold X, is a generator of the homology group
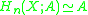 , and we set
, and we set
where
 is the inclusion homomorphism.
is the inclusion homomorphism.To define an absolute filling radius in a situation where X is equipped with a Riemannian metric g, Gromov proceeds as follows. One exploits an imbedding due to Kazimierz Kuratowski
Kazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
(the first name is sometimes spelled with a "C"). One imbeds X in the Banach space
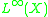 of bounded Borel functions on X, equipped with the sup norm . Namely, we map a point
of bounded Borel functions on X, equipped with the sup norm . Namely, we map a point 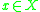 to the function
to the function  defined by the formula
defined by the formula 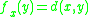
for all
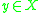 , where d is the distance function defined by the metric. By the triangle inequality we have
, where d is the distance function defined by the metric. By the triangle inequality we have 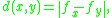 and therefore the imbedding is strongly isometric, in the precise sense that internal distance and ambient distance coincide. Such a strongly isometric imbedding is impossible if the ambient space is a Hilbert space, even when X is the Riemannian circle (the distance between opposite points must be
and therefore the imbedding is strongly isometric, in the precise sense that internal distance and ambient distance coincide. Such a strongly isometric imbedding is impossible if the ambient space is a Hilbert space, even when X is the Riemannian circle (the distance between opposite points must beπ, not 2!). We then set
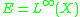 in the formula above, and define
in the formula above, and define
Relation to diameter and systole
The exact value of the filling radius is known in very few cases. A general inequality relating the filling radius and the Riemannian diameter of X was proved in (Katz, 1983): the filling radius is at most a third of the diameter. In some cases, this yields the precise value of the filling radius. Thus, the filling radius of the Riemannian circle of length 2π, i.e. the unit circle with the induced Riemannian distance function, equals π/3, i.e. a sixth of its length. This follows by combing the diameter upper bound mentioned above with Gromov's lower bound in terms of the systole (Gromov, 1983). More generally, the filling radius of real projective spaceReal projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
with a metric of constant curvature is a third of its Riemannian diameter, see (Katz, 1983). Equivalently, the filling radius is a sixth of the systole in these cases. The precise value is also known for the n-spheres (Katz, 1983).
The filling radius is linearly related to the systole of an essential manifold
Essential manifold
In mathematics, in algebraic topology and differential geometry, the notion of an essential manifold seems to have been first introduced explicitly in Mikhail Gromov's classic text in 1983 .-Definition:...
M. Namely, the systole of such an M is at most six times its filling radius, see (Gromov, 1983). The inequality is optimal in the sense that the boundary case of equality is attained by the real projective spaces as above.

