Fano's inequality
Encyclopedia
In information theory
, Fano's inequality (also known as the Fano converse and the Fano lemma) relates the average information lost in a noisy channel to the probability of the categorization error. It was derived by Robert Fano
in the early 1950s while teaching a Ph.D.
seminar in information theory at MIT, and later recorded in his 1961 textbook.
It is used to find a lower bound on the error probability of any decoder
as well as the lower bounds for minimax risks in density estimation
.
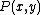. Fano's inequality is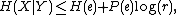
where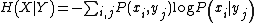
is the conditional entropy
,
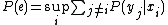
is the probability of the communication error, and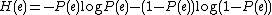
is the corresponding binary entropy.
with density
equal to one of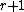
possible densities 
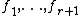. Furthermore, the Kullback-Leibler divergence between any pair of densities cannot be too large,
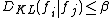for all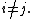 
Let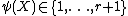
be an estimate of the index. Then
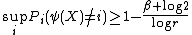
where
is the probability
induced by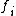
Let F be a class of densities with a subclass of r + 1 densities ƒθ such that for any θ ≠ θ′
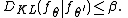
Then in the worst case the expected value
of error of estimation is bound from below,
where ƒn is any density estimator
based on a sample
of size n.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, Fano's inequality (also known as the Fano converse and the Fano lemma) relates the average information lost in a noisy channel to the probability of the categorization error. It was derived by Robert Fano
Robert Fano
Robert Mario Fano is an Italian-American computer scientist, currently professor emeritus of Electrical Engineering and Computer Science at Massachusetts Institute of Technology. Fano is known principally for his work on information theory, inventing Shannon-Fano coding...
in the early 1950s while teaching a Ph.D.
Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
seminar in information theory at MIT, and later recorded in his 1961 textbook.
It is used to find a lower bound on the error probability of any decoder
Decoder
A decoder is a device which does the reverse operation of an encoder, undoing the encoding so that the original information can be retrieved. The same method used to encode is usually just reversed in order to decode...
as well as the lower bounds for minimax risks in density estimation
Density estimation
In probability and statistics,density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function...
.
Fano's inequality
Let the random variables X and Y represent input and output messages (out of r+1 possible messages) with a joint probability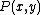. Fano's inequality is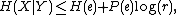where
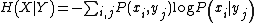
is the conditional entropy
Conditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
,
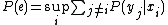
is the probability of the communication error, and
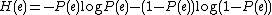
is the corresponding binary entropy.
Alternative formulation
Let X be a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with density
Probability density
Probability density may refer to:* Probability density function in probability theory* The product of the probability amplitude with its complex conjugate in quantum mechanics...
equal to one of
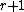possible densities 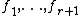. Furthermore, the Kullback-Leibler divergence between any pair of densities cannot be too large, 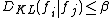for all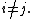 Let
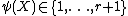be an estimate of the index. Then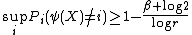where
is the probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
induced by
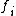
Generalization
The following generalization is due to Ibragimov and Khasminskii (1979), Assouad and Birge (1983).Let F be a class of densities with a subclass of r + 1 densities ƒθ such that for any θ ≠ θ
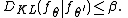
Then in the worst case the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of error of estimation is bound from below,
where ƒn is any density estimator
Density estimation
In probability and statistics,density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function...
based on a sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
of size n.