
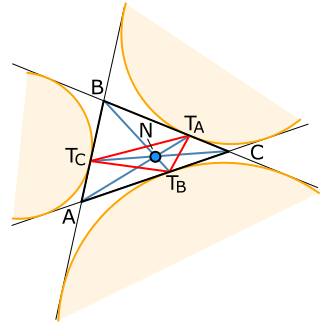
Extouch triangle
Encyclopedia
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
by:
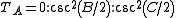
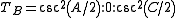
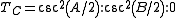
Or, equivalently, where a,b,c are the lengths of the sides opposite angles A, B, C respectively,
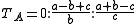
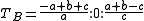
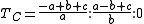
The intersection of the lines connecting the vertices of the original triangle to the corresponding vertices of the extouch triangle is the Nagel point
Nagel point
In geometry, the Nagel point is a point associated with any triangle. Given a triangle ABC, let TA, TB, and TC be the extouch points in which the A-excircle meets line BC, the B-excircle meets line CA, and C-excircle meets line AB, respectively...
. This is shown in blue and labelled "N" in the diagram.
Area
The area of the extouch triangle,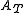 , is given by:
, is given by:
where
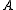 ,
,  ,
,  are the area, radius of the incircle and semiperimeter
are the area, radius of the incircle and semiperimeterSemiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
of the original triangle, and
 ,
, 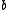 ,
,  are the side lengths of the original triangle.
are the side lengths of the original triangle.This is the same area as the intouch triangle.

