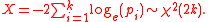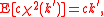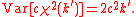Extensions of Fisher's method
Encyclopedia
In statistics
, extensions of Fisher's method are a group of approaches that allow approximately valid statistical inference
s to be made when the assumptions required for the direct application of Fisher's method
are not valid. Fisher's method is a way of combining the information in the p-values from different statistical tests
so as to form a single overall test: this method requires that the individual test statistics (or, more immediately, their resulting p-values) should be statistically independent
.
is its exclusive design to combine independent p-values, which renders it an unreliable technique to combine dependent p-values. To overcome this limitation, a number of methods were developed to extend its utility.
s follow a χ2-distribution with 2k degrees of freedom:
In the case that these p-values are not independent, Brown proposed the idea of approximating X using a scaled χ2-distribution, cχ2(k’), with k’ degrees of freedom.
The mean and variance of this scaled χ2 variable are:
This approximation is shown to be accurate up to two moments.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, extensions of Fisher's method are a group of approaches that allow approximately valid statistical inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
s to be made when the assumptions required for the direct application of Fisher's method
Fisher's Method
In statistics, Fisher's method, also known as Fisher's combined probability test, is a technique for data fusion or "meta-analysis" . It was developed by and named for Ronald Fisher...
are not valid. Fisher's method is a way of combining the information in the p-values from different statistical tests
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
so as to form a single overall test: this method requires that the individual test statistics (or, more immediately, their resulting p-values) should be statistically independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
.
Dependent statistics
A principle limitation of Fisher's methodFisher's Method
In statistics, Fisher's method, also known as Fisher's combined probability test, is a technique for data fusion or "meta-analysis" . It was developed by and named for Ronald Fisher...
is its exclusive design to combine independent p-values, which renders it an unreliable technique to combine dependent p-values. To overcome this limitation, a number of methods were developed to extend its utility.
Brown's method
Fisher's method showed that the log-sum of k independent p-valueP-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
s follow a χ2-distribution with 2k degrees of freedom:
In the case that these p-values are not independent, Brown proposed the idea of approximating X using a scaled χ2-distribution, cχ2(k’), with k’ degrees of freedom.
The mean and variance of this scaled χ2 variable are:
This approximation is shown to be accurate up to two moments.