Exponential random graph model
Encyclopedia
The exponential random graph model (ERGM) is a powerful and flexible statistical model for networks.
Formally a random graph
consists of a set of 
nodes and 
dyads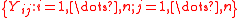 
where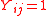 
if the nodes 
are connected and 
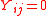otherwise.
The basic assumption of this model is that the structure in an observed graph
can be explained by a set of network configurations or "network statistics"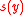 
(for instance, the number of edges, 2-stars, triangles, etc.)
The model represents the probability of observing a given graph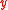
and has the following form:
where
Formally a random graph
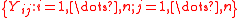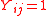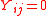consists of a set of nodes and dyads where if the nodes are connected and otherwise.The basic assumption of this model is that the structure in an observed graph
can be explained by a set of network configurations or "network statistics" 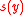(for instance, the number of edges, 2-stars, triangles, etc.)The model represents the probability of observing a given graph
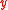and has the following form:where
is the vector of model parameters,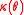
is a normalizing constant which is intractable for non-trivially small networks.
Further reading
- Garry Robins, Pip Pattison, Yuval Kalish, Dean Lusher, An Introduction to Exponential Random Graph (p*) Models for Social Networks
- http://www.stat.psu.edu/~dhunter/talks/ergm.pdf
- Exponential families