
Exact statistics
Encyclopedia
Exact statistics, such as that described in exact test
, is a branch of statistics
that was developed to provide more accurate results pertaining to statistical testing and interval estimation
by eliminating procedures based on asymptotic
and approximate statistical methods. The main characteristic of exact methods is that statistical tests and confidence interval
s are based on exact probability statements that are valid for any sample size
.
Exact statistical methods help avoid some of the unreasonable assumptions of traditional statistical methods, such as the assumption of equal variances in classical ANOVA. They also allow exact inference on variance components of mixed model
s.
When exact p-values and confidence intervals are computed under a certain distribution, such as the normal distribution, then the underlying methods are referred to as exact parametric methods. The exact methods that do not make any distributional assumptions are referred to as exact nonparametric methods. The latter has the advantage of making fewer assumptions whereas, the former tend to yield more powerful tests when the distributional assumption is reasonable. For advanced methods such as higher-way ANOVA regression analysis
, and mixed models, only exact parametric methods are available.
When the sample size is small, asymptotic results given by some traditional methods may not be valid. In such situations, the asymptotic p-value
s may differ substantially from the exact p-values. Hence asymptotic and other approximate results may lead to unreliable and misleading conclusions.
 and variance
and variance  , suppose
, suppose  and
and 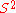 are the sample mean and the sample variance. Then, it is well known that
are the sample mean and the sample variance. Then, it is well known that
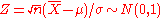
and that
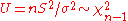 .
.
Now suppose the parameter of interest is the coefficient of variation, . Then, we can easily perform exact tests and exact confidence intervals for
. Then, we can easily perform exact tests and exact confidence intervals for  based on the generalized statistic
based on the generalized statistic
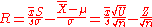 ,
,
where is the observed value of
is the observed value of  and
and  is the observed value of
is the observed value of  . Exact inferences on
. Exact inferences on  based on probabilities and expected values of
based on probabilities and expected values of  are possible because its distribution and the observed value are both free of nuisance parameters.
are possible because its distribution and the observed value are both free of nuisance parameters.
s are defined as an extension of the classical p-values so that one can perform tests based on exact probability statements valid for any sample size.
Exact test
In statistics, an exact test is a test where all assumptions upon which the derivation of the distribution of the test statistic is based are met, as opposed to an approximate test, in which the approximation may be made as close as desired by making the sample size big enough...
, is a branch of statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
that was developed to provide more accurate results pertaining to statistical testing and interval estimation
Interval estimation
In statistics, interval estimation is the use of sample data to calculate an interval of possible values of an unknown population parameter, in contrast to point estimation, which is a single number. Neyman identified interval estimation as distinct from point estimation...
by eliminating procedures based on asymptotic
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
and approximate statistical methods. The main characteristic of exact methods is that statistical tests and confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s are based on exact probability statements that are valid for any sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
.
Exact statistical methods help avoid some of the unreasonable assumptions of traditional statistical methods, such as the assumption of equal variances in classical ANOVA. They also allow exact inference on variance components of mixed model
Mixed model
A mixed model is a statistical model containing both fixed effects and random effects, that is mixed effects. These models are useful in a wide variety of disciplines in the physical, biological and social sciences....
s.
When exact p-values and confidence intervals are computed under a certain distribution, such as the normal distribution, then the underlying methods are referred to as exact parametric methods. The exact methods that do not make any distributional assumptions are referred to as exact nonparametric methods. The latter has the advantage of making fewer assumptions whereas, the former tend to yield more powerful tests when the distributional assumption is reasonable. For advanced methods such as higher-way ANOVA regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, and mixed models, only exact parametric methods are available.
When the sample size is small, asymptotic results given by some traditional methods may not be valid. In such situations, the asymptotic p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
s may differ substantially from the exact p-values. Hence asymptotic and other approximate results may lead to unreliable and misleading conclusions.
The Approach
All classical statistical procedures are constructed using statistics which depend only on observable random vectors, whereas Generalized Estimators, Tests, and Confidence Intervals used in exact statistics take advantage of the observable random vectors and the observed values both, as in the Bayesian approach but without having to treat constant parameters as random variables. For example, in sampling from a normal population with mean and variance
and variance  , suppose
, suppose  and
and 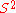 are the sample mean and the sample variance. Then, it is well known that
are the sample mean and the sample variance. Then, it is well known that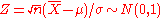
and that
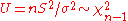 .
.Now suppose the parameter of interest is the coefficient of variation,
 . Then, we can easily perform exact tests and exact confidence intervals for
. Then, we can easily perform exact tests and exact confidence intervals for  based on the generalized statistic
based on the generalized statistic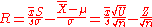 ,
,where
 is the observed value of
is the observed value of  and
and  is the observed value of
is the observed value of  . Exact inferences on
. Exact inferences on  based on probabilities and expected values of
based on probabilities and expected values of  are possible because its distribution and the observed value are both free of nuisance parameters.
are possible because its distribution and the observed value are both free of nuisance parameters.Generalized p-values
Classical statistical methods do not provide exact tests to many statistical problems such as testing Variance Components and ANOVA under unequal variances. To rectify this situation, the generalized p-valueGeneralized p-value
In statistics, a generalized p-value is an extended version of the classical p-value, which except in a limited number of applications, provide only approximate solutions....
s are defined as an extension of the classical p-values so that one can perform tests based on exact probability statements valid for any sample size.
External links
- XPro, Free software package for exact parametric statistics

