
Euler's theorem in geometry
Encyclopedia
In geometry
, Euler's theorem, named after Leonhard Euler
, states that the distance d between the circumcentre and incentre of a triangle
can be expressed as
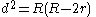
where R and r denote the circumradius and inradius respectively (the radii of the above two circles).
From the theorem follows the Euler inequality: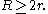
therefore angle BIL = angle IBL, so BL = IL, and AI × IL = 2Rr. Extend OI so that it intersects the circumcircle at P and Q, then PI × QI = AI × IL = 2Rr, so (R + d)(R − d) = 2Rr, i.e. d2 = R(R − 2r).
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Euler's theorem, named after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, states that the distance d between the circumcentre and incentre of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
can be expressed as
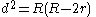
where R and r denote the circumradius and inradius respectively (the radii of the above two circles).
From the theorem follows the Euler inequality:
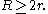
Proof
Let O be the circumcentre of triangle ABC, and I be its incentre, the extension of AI intersects the circumcircle at L, then L is the mid-point of arc BC. Join LO and extend it so that it intersects the circumcircle at M. From I construct a perpendicular to AB, and let D be its foot, then ID = r. It is not difficult to prove that triangle ADI is similar to triangle MBL, so ID / BL = AI / ML, i.e. ID × ML = AI × BL. Therefore 2Rr = AI × BL. Join BI, because- angle BIL = angle A / 2 + angle ABC / 2,
- angle IBL = angle ABC / 2 + angle CBL = angle ABC / 2 + angle A / 2,
therefore angle BIL = angle IBL, so BL = IL, and AI × IL = 2Rr. Extend OI so that it intersects the circumcircle at P and Q, then PI × QI = AI × IL = 2Rr, so (R + d)(R − d) = 2Rr, i.e. d2 = R(R − 2r).
See also
- Bicentric quadrilateral#Fuss' theorem and Carlitz' identity for the relation among the same three variables in bicentric quadrilaterals

