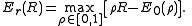Error exponent
Encyclopedia
In information theory
, the error exponent of a channel code
or source code
over the block length of the code is the logarithm of the error probability. For example, if the probability of error of a decoder
drops as e–nα, where n is the block length, the error exponent is α. Many of the information-theoretic
theorems are of asymptotic nature, for example, the channel coding theorem
states that for any rate less than the channel capacity, the probability of the error of the channel code can made to go to zero as the block length goes to infinity. In practical situations, there are limitations to the delay of the communication and the block length of the code cannot be taken to go to infinity. Therefore it is important to study how the probability of error drops as the block length go to infinity.
states that for any ε > 0 and for any rate less than the channel capacity, there is an encoding and decoding scheme that can be used to ensure that the probability of block error is less than ε > 0 for sufficiently long message block X. Also, for any rate greater than the channel capacity, the probability of block error at the receiver goes to one as the block length goes to infinity.
Assuming a channel coding setup as follows: the channel can transmit any of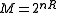
messages, by transmitting the corresponding codeword (which is of length n). Each component in the codebook is drawn i.i.d. according to some probability distribution with probability mass function
Q. At the decoding end, ML decoding is done.
Given that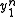
is received, X(1) or first message is transmitted, the probability that X(1) is incorrectly detected as X(2) is:
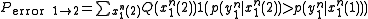
The function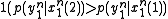
has upper bound
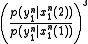
for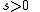
Thus,
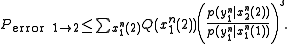
Since there are a total of M messages, the Probability that X(1) is confused with any other message is M times the above expression. Since each entry in the codebook is i.i.d., the notation of X(2) can be replaced simply by X. Using the Hokey union bound, the probability of confusing X(1) with any message is bounded by:
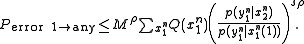
Averaging over all combinations of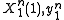
:
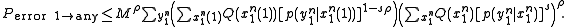
Choosing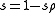
and combining the two sums over 
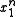in the above formula:
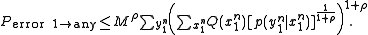
Using the independence nature of the elements of the codeword, and the discrete memoryless nature of the channel:
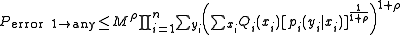
Using the fact that each element of codeword is identically distributed and thus stationary:
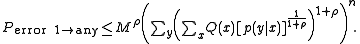
Replacing M by 2nR and defining
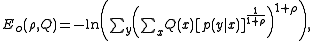
probability of error becomes
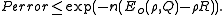
Q and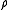
should be chosen so that the bound is tighest. Thus, the error exponent can be defined as
theorem states that for any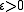
and any discrete-time i.i.d. source such as 
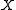and for any rate less than the entropy
of the source, there is large enough
and an encoder that takes 
i.i.d. repetition of the source,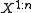 
, and maps it to 
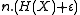binary bits such that the source symbols 
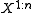are recoverable from the binary bits with probability at least 
.
Let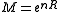
be the total number of possible messages. Next map each of the possible source output sequences to one of the messages randomly using a uniform distribution and independently from everything else. When a source is generated the corresponding message 
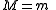is then transmitted to the destination. The message gets decoded to one of the possible source strings. In order to minimize the probability of error the decoder will decode to the source sequence 
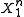that maximizes 
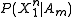, where 
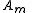denotes the event that message 
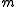was transmitted. This rule is equivalent to finding the source sequence 
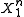among the set of source sequences that map to message 
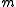that maximizes 
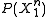. This reduction follows from the fact that the messages were assigned randomly and independently of everything else.
Thus, as an example of when an error occurs, supposed that the source sequence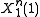
was mapped to message 
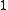as was the source sequence 
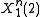. If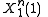 
was generated at the source, but 
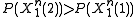then an error occurs.
Let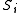
denote the event that the source sequence 
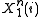was generated at the source, so that 
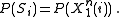Then the probability of error can be broken down as 
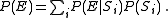Thus, attention can be focused on finding an upper bound to the 
.
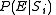Let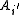
denote the event that the source sequence 
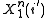was mapped to the same message as the source sequence 
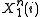and that 
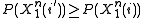. Thus, letting 
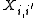denote the event that the two source sequences 
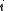and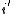 
map to the same message, we have that
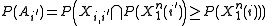
and using the fact that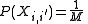
and is independent of everything else have that
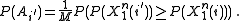
A simple upper bound for the term on the left can be established as
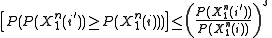
for some arbitrary real number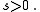
This upper bound can be verified by noting that 
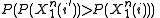either equals 
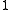or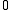 
because the probabilities of a given input sequence are completely deterministic. Thus, if 
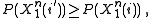then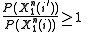 
so that the inequality holds in that case. The inequality holds in the other case as well because
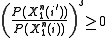
for all possible source strings. Thus, combining everything and introducing some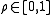
, have that
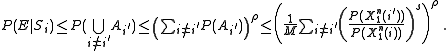
Where the inequalities follow from a variation on the Union Bound. Finally applying this upper bound to the summation for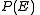
have that:
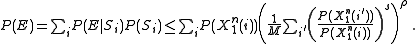
Where the sum can now be taken over all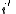
because that will only increase the bound. Ultimately yielding that
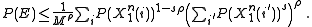
Now for simplicity let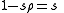
so that 
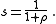Substituting this new value of 
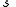into the above bound on the probability of error and using the fact that 
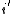is just a dummy variable in the sum gives the following as an upper bound on the probability of error:
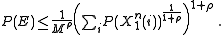
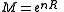and each of the components of 
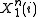are independent. Thus, simplifying the above equation yields
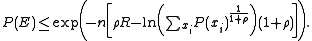
The term in the exponent should be maximized over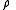
in order to achieve the tightest upper bound on the probability of error.
Letting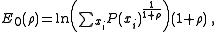
see that the error exponent for the source coding case is:
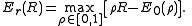
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, the error exponent of a channel code
Channel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
or source code
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
over the block length of the code is the logarithm of the error probability. For example, if the probability of error of a decoder
Decoder
A decoder is a device which does the reverse operation of an encoder, undoing the encoding so that the original information can be retrieved. The same method used to encode is usually just reversed in order to decode...
drops as e–nα, where n is the block length, the error exponent is α. Many of the information-theoretic
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
theorems are of asymptotic nature, for example, the channel coding theorem
Noisy channel coding theorem
In information theory, the noisy-channel coding theorem , establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data nearly error-free up to a computable maximum rate through the channel...
states that for any rate less than the channel capacity, the probability of the error of the channel code can made to go to zero as the block length goes to infinity. In practical situations, there are limitations to the delay of the communication and the block length of the code cannot be taken to go to infinity. Therefore it is important to study how the probability of error drops as the block length go to infinity.
For time-invariant DMC channels
The channel coding theoremNoisy channel coding theorem
In information theory, the noisy-channel coding theorem , establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data nearly error-free up to a computable maximum rate through the channel...
states that for any ε > 0 and for any rate less than the channel capacity, there is an encoding and decoding scheme that can be used to ensure that the probability of block error is less than ε > 0 for sufficiently long message block X. Also, for any rate greater than the channel capacity, the probability of block error at the receiver goes to one as the block length goes to infinity.
Assuming a channel coding setup as follows: the channel can transmit any of
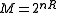messages, by transmitting the corresponding codeword (which is of length n). Each component in the codebook is drawn i.i.d. according to some probability distribution with probability mass functionProbability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
Q. At the decoding end, ML decoding is done.
Given that
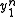is received, X(1) or first message is transmitted, the probability that X(1) is incorrectly detected as X(2) is: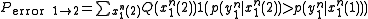The function
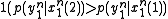has upper bound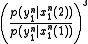for
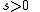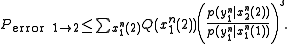
Thus,Since there are a total of M messages, the Probability that X(1) is confused with any other message is M times the above expression. Since each entry in the codebook is i.i.d., the notation of X(2) can be replaced simply by X. Using the Hokey union bound, the probability of confusing X(1) with any message is bounded by:
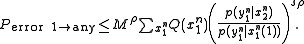
Averaging over all combinations of
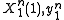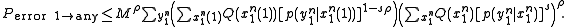
:Choosing
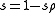and combining the two sums over 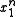in the above formula: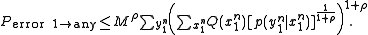Using the independence nature of the elements of the codeword, and the discrete memoryless nature of the channel:
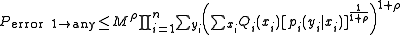
Using the fact that each element of codeword is identically distributed and thus stationary:
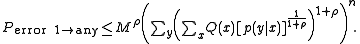
Replacing M by 2nR and defining
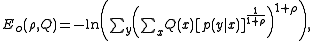
probability of error becomes
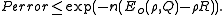
Q and
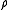should be chosen so that the bound is tighest. Thus, the error exponent can be defined as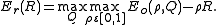For time invariant discrete memoryless sources
The source codingSource coding
In information theory, Shannon's source coding theorem establishes the limits to possible data compression, and the operational meaning of the Shannon entropy....
theorem states that for any
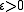and any discrete-time i.i.d. source such as 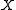and for any rate less than the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the source, there is large enough
and an encoder that takes i.i.d. repetition of the source, 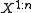, and maps it to 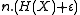binary bits such that the source symbols 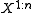are recoverable from the binary bits with probability at least .Let
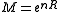be the total number of possible messages. Next map each of the possible source output sequences to one of the messages randomly using a uniform distribution and independently from everything else. When a source is generated the corresponding message 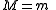is then transmitted to the destination. The message gets decoded to one of the possible source strings. In order to minimize the probability of error the decoder will decode to the source sequence 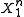that maximizes 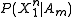, where 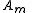denotes the event that message 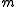was transmitted. This rule is equivalent to finding the source sequence 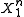among the set of source sequences that map to message 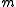that maximizes 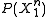. This reduction follows from the fact that the messages were assigned randomly and independently of everything else.Thus, as an example of when an error occurs, supposed that the source sequence
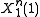was mapped to message 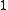as was the source sequence 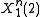. If 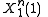was generated at the source, but 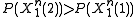then an error occurs.Let
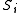denote the event that the source sequence 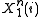was generated at the source, so that 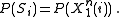Then the probability of error can be broken down as 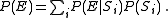Thus, attention can be focused on finding an upper bound to the 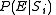.Let
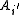denote the event that the source sequence 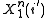was mapped to the same message as the source sequence 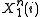and that 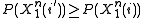. Thus, letting 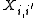denote the event that the two source sequences 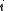and 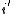map to the same message, we have that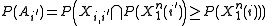and using the fact that
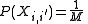and is independent of everything else have that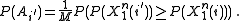A simple upper bound for the term on the left can be established as
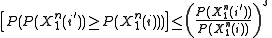
for some arbitrary real number
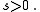This upper bound can be verified by noting that 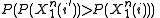either equals 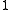or 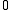because the probabilities of a given input sequence are completely deterministic. Thus, if 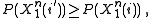then 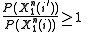so that the inequality holds in that case. The inequality holds in the other case as well because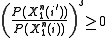for all possible source strings. Thus, combining everything and introducing some
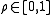, have that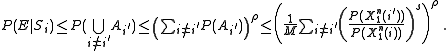Where the inequalities follow from a variation on the Union Bound. Finally applying this upper bound to the summation for
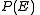have that: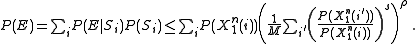Where the sum can now be taken over all
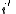because that will only increase the bound. Ultimately yielding that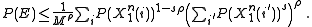Now for simplicity let
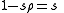so that 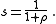Substituting this new value of 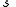into the above bound on the probability of error and using the fact that 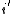is just a dummy variable in the sum gives the following as an upper bound on the probability of error: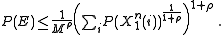 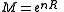and each of the components of 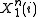are independent. Thus, simplifying the above equation yields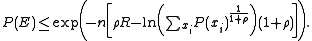The term in the exponent should be maximized over
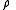in order to achieve the tightest upper bound on the probability of error.Letting
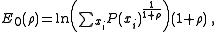see that the error exponent for the source coding case is: