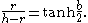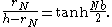In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the equal incircles theorem derives from a Japanese Sangaku

Sangaku

Sangaku or San Gaku are Japanese geometrical puzzles in Euclidean geometry on wooden tablets which were placed as offerings at Shinto shrines or Buddhist temples during the Edo period by members of all social classes.-History:The Sangaku were painted in color on wooden tablets and hung in the...

, and pertains to the following construction: a series of rays are drawn from a given point to a given line such that the inscribed circles of the triangles formed by adjacent rays and the base line are equal. In the illustration the equal blue circles define the spacing between the rays, as described.

The theorem states that the incircles of the triangles formed (starting from any given ray) by every other ray, every third ray, etc. and the base line are also equal. The case of every other ray is illustrated above by the green circles, which are all equal.

From the fact that the theorem doesn't depend on the angle of the initial ray, it can be seen that the theorem properly belongs to analysis, rather than geometry, and must relate to a continuous scaling function which defines the spacing of the rays. In fact, this function is the hyperbolic sine

Hyperbolic function

In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...

.

The theorem is a trivial corollary of the following lemma:

Suppose that the nth ray makes an angle 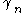with the normal to the baseline. If is parameterized according to the equation, 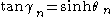, then values of , where and 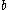are real constants, define a sequence of rays that satisfy the condition of equal incircles, and furthermore any sequence of rays satisfying the condition can be produced by suitable choice of the constants and .

Proof of the lemma

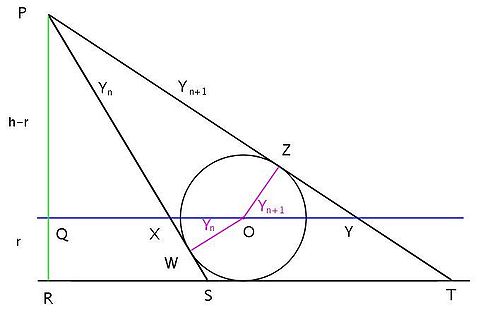
In the diagram, lines PS and PT are adjacent rays making angles and 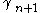with line PR, which is perpendicular to the baseline, RST.

Line QXOY is parallel to the baseline and passes through O, the center of the incircle of PST, which is tangent to the rays at W and Z. Also, line PQ has length , and line QR has length , the radius of the incircle.

Then OWX is similar to PQX and OZY is similar to PQY, and from XY = XO + OY we get

This relation on a set of angles, , expresses the condition of equal incircles.

To prove the lemma, we set 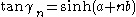, which gives .

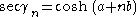Using 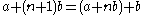, we apply the addition rules for 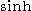and , and verify that the equal incircles relation is satisfied by setting

This gives an expression for the parameter 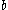in terms of the geometric measures, 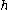and . With this definition of 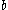we then obtain an expression for the radii, 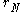, of the incircles formed by taking every Nth ray as the sides of the triangles

See also

• Hyperbolic function
  Hyperbolic function
  In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
  
  
• Japanese theorem for cyclic polygons
• Japanese theorem for cyclic quadrilaterals
• Tangent lines to circles
  Tangent lines to circles
  In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...