
Epicyclic gearing
Encyclopedia

Gear
A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....
system consisting of one or more outer gears, or planet gears, revolving about a central, or sun gear. Typically, the planet gears are mounted on a movable arm or carrier which itself may rotate relative to the sun gear. Epicyclic gearing systems also incorporate the use of an outer ring gear or annulus, which meshes with the planet gears. Planetary gears (or epicyclic gears) are typically classified as simple and compound planetary gears. Simple planetary gears have one sun, one ring, one carrier, and one planet set. Compound planetary gears involve one or more of the following three types of structures: meshed-planet (there are at least two more more planets in mesh with each other in each planet train), stepped-planet (there exists a shaft connection between two planets in each planet
train), and multi-stage structures (the system contains two or more planet sets). Compared to simple planetary gears, compound planetary gears have the advantages of larger reduction ratio, higher torque-to-weight ratio, and more flexible configurations.
The axes of all gears are usually parallel, but for special cases like pencil sharpeners they can be placed at an angle, introducing elements of bevel gear
Bevel gear
Bevel gears are gears where the axes of the two shafts intersect and the tooth-bearing faces of the gears themselves are conically shaped.Bevel gears are most often mounted on shafts that are 90 degrees apart, but can be designed to work at other angles as well...
(see below). Further, the sun, planet carrier and annulus axes are usually concentric
Concentric
Concentric objects share the same center, axis or origin with one inside the other. Circles, tubes, cylindrical shafts, disks, and spheres may be concentric to one another...
.
Gear ratio

Gear ratio
The gear ratio of a gear train is the ratio of the angular velocity of the input gear to the angular velocity of the output gear, also known as the speed ratio of the gear train. The gear ratio can be computed directly from the numbers of teeth of the various gears that engage to form the gear...
in an epicyclic gearing system is somewhat non-intuitive, particularly because there are several ways in which an input rotation can be converted into an output rotation. The three basic components of the epicyclic gear are:
- Sun: The central gear
- Planet carrier: Holds one or more peripheral planet gears, all of the same size, meshed with the sun gear
- Annulus: An outer ring with inward-facing teeth that mesh with the planet gear or gears
In many epicyclic gearing systems, one of these three basic components is held stationary; one of the two remaining components is an input, providing power to the system, while the last component is an output, receiving power from the system. The ratio of input rotation to output rotation is dependent upon the number of teeth in each gear, and upon which component is held stationary.
In other systems, such as hybrid vehicle transmissions, two of the components are used as inputs with the third providing output relative to the two inputs.
In one arrangement, the planetary carrier (green) is held stationary, and the sun gear (yellow) is used as input. In this case, the planetary gears simply rotate about their own axes (ie, spin) at a rate determined by the number of teeth in each gear. If the sun gear has Ns teeth, and each planet gear has Np teeth, then the ratio is equal to -Ns/Np. For instance, if the sun gear has 24 teeth, and each planet has 16 teeth, then the ratio is -24/16, or -3/2; this means that one clockwise turn of the sun gear produces 1.5 counterclockwise turns of each of the planet gear(s) about its axis.
This rotation of the planet gears can in turn drive the annulus (not depicted in diagram), in a corresponding ratio. If the annulus has Na teeth, then the annulus will rotate by Np/Na turns for each turn of the planet gears. For instance, if the annulus has 64 teeth, and the planets 16, one clockwise turn of a planet gear results in 16/64, or 1/4 clockwise turns of the annulus. Extending this case from the one above:
- One turn of the sun gear results in
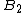 turns of the planets
turns of the planets - One turn of a planet gear results in
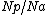 turns of the annulus
turns of the annulus
So, with the planetary carrier locked, one turn of the sun gear results in
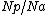 turns of the annulus.
turns of the annulus.The annulus may also be held fixed, with input provided to the planetary gear carrier; output rotation is then produced from the sun gear. This configuration will produce an increase in gear ratio, equal to 1+Na/Ns.
These are all described by the equation:
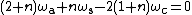
where n is the form factor of the planetary gear, defined by:
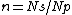
If the annulus is held stationary and the sun gear is used as the input, the planet carrier will be the output. The gear ratio in this case will be 1/(1+Na/Ns). This is the lowest gear ratio attainable with an epicyclic gear train. This type of gearing is sometimes used in tractors and construction equipment to provide high torque to the drive wheels.
In bicycle hub gear
Hub gear
A hub gear, internal-gear hub, or just gear hub is a gear ratio changing system commonly used on bicycles that is implemented with planetary or epicyclic gears. The gears and lubricants are sealed within the hub-shell of the bicycle's rear wheel, as opposed to derailleur gears, where the gears and...
s, the sun is usually stationary, being keyed to the axle or even machined directly onto it. The planetary gear carrier is used as input. In this case the gear ratio is simply given by (Ns+Na)/Na. The number of teeth in the planet gear is irrelevant.

Compound planetary gears
"Compound planetary gear" is a general concept and it refers to any planetary gears involve one or more of the following three types of structures: meshed-planet (there are at least two more planets in mesh with each other in each planet train), stepped-planet (there exists a shaft connection between two planets in each planettrain), and multi-stage structures (the system contains two or more planet sets).
Some designs use "stepped-planet" which have two differently-sized gears on either end of a common casting. The large end engages the sun, while the small end engages the annulus. This may be necessary to achieve smaller step changes in gear ratio when the overall package size is limited. Compound planets have "timing marks" (or "relative gear mesh phase" in technical term). The assembly conditions of compound planetary gears are more restrictive then simple planetary gears, and they must be assembled in the correct initial orientation relative to each other, or their teeth will not simultaneously engage the sun and annulus at opposite ends of the planet, leading to very rough running and short life. Compound planetary gears can easily achieve larger transmission ratio with equal or smaller volume. For example, compound planets with teeth in a 2:1 ratio with a 50T annulus would give the same effect as a 100T annulus, but with half the actual diameter.
More planet and sun gear units can be placed in series in the same annulus housing (where the output shaft of the first stage becomes the input shaft of the next stage) providing a larger (or smaller) gear ratio. This is the way some automatic transmission
Automatic transmission
An automatic transmission is one type of motor vehicle transmission that can automatically change gear ratios as the vehicle moves, freeing the driver from having to shift gears manually...
s work.
During World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
, a special variation of epicyclic gearing was developed for portable radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
gear, where a very high reduction ratio in a small package was needed. This had two outer annular gears, each half the thickness of the other gears. One of these two annular gears was held fixed and had one tooth fewer than did the other. Therefore, several turns of the "sun" gear made the "planet" gears complete a single revolution, which in turn made the rotating annular gear rotate by a single tooth.
Calculating the output from the input
It is first drawn simplified as the sun, a single planet, the annulus, and an arm holding the planet (a simple planetary gear). Any gear can be the input or output, including the arm.Now, put in the known values and solve for
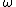 ring:
ring: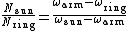
or you can use the other form of this equation:
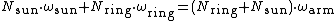
where N is the number of teeth,
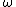 is angular velocity
is angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the element (sun, arm, or ring). Since the angular velocity and rpm are directly proportional, you can use rpm instead.
However, if the arm is the input or output, say the ring is the output/input instead and reverse the direction (since if the arm moves a certain speed relative to the ring, the ring moves that same speed the other way relative to the arm, and obviously the arm does not have a tooth count to plug in)
To derive this, just imagine the arm is locked, and calculate the gear ratio
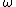 ring /
ring / 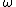 sun = Nsun / Nring, then unlock the arm. From the arms reference frame the ratio is always Nsun/Nring, but from your frame all the speeds are increased by the angular velocity of the arm. So to write this relative relationship, you arrive at the equation from above.
sun = Nsun / Nring, then unlock the arm. From the arms reference frame the ratio is always Nsun/Nring, but from your frame all the speeds are increased by the angular velocity of the arm. So to write this relative relationship, you arrive at the equation from above.Also, make sure Nsun+2Nplanet=Nring where N is the number of teeth. This simply says that the gears will fit, since N is directly proportional to diameter.
Formulas for calculating gear ratios
| Name | Number of teeth | Speed |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
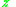 |
 |
| Sketch | Output speed | Sketch | Output speed | Sketch | Output speed | Sketch | Output speed |
|---|---|---|---|---|---|---|---|
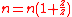 |
 |
 |
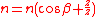 |
||||
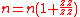 |
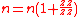 |
 |
 |
||||
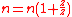 |
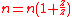 |
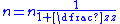 |
 |
||||
 |
 |
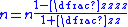 |
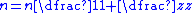 |
||||
 |
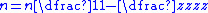 |
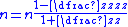 |
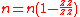 |
||||
 |
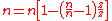 |
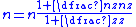 |
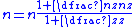 |
Advantages and disadvantages
Advantages of planetary gears over parallel axis gears include high power density, large reduction in a small volume, multiple kinematic combinations, pure torsional reactions, and coaxial shafting. Disadvantages include high bearing loads, inaccessibility, and design complexity.The planetary gearbox arrangement is an engineering design that offers many advantages over traditional gearbox arrangements. One advantage is its unique combination of both compactness and outstanding power transmission efficiencies. A typical efficiency loss in a planetary gearbox arrangement is only 3% per stage. This type of efficiency ensures that a high proportion of the energy being input is transmitted through the gearbox, rather than being wasted on mechanical losses inside the gearbox.
Another advantage of the planetary gearbox arrangement is load distribution. Because the load being transmitted is shared between multiple planets, torque capability is greatly increased. The more planets in the system, the greater load ability and the higher the torque density.
The planetary gearbox arrangement also creates greater stability due to the even distribution of mass and increased rotational stiffness.
See also
- Continuously variable transmissionContinuously variable transmissionA continuously variable transmission is a transmission that can change steplessly through an infinite number of effective gear ratios between maximum and minimum values. This contrasts with other mechanical transmissions that offer a fixed number of gear ratios...
(CVT) - Cycloidal driveCycloidal driveA cycloidal drive or cycloidal speed reducer is a mechanism for reducing the speed of an input shaft by a certain ratio. Cycloidal speed reducers are capable of high ratios in compact sizes....
- EpicycloidEpicycloidIn geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
- Ford Model TFord Model TThe Ford Model T is an automobile that was produced by Henry Ford's Ford Motor Company from September 1908 to May 1927...
- NuVinci gearing
- Ravigneaux planetary gearsetRavigneaux planetary gearsetThe Ravigneaux gearset is a double planetary gear set commonly used in automatic transmissions. This planetary gear set is constructed from two gear pairs, ring-planet and planet-planet. The Ravigneaux set has two sun gear wheels, a large sun and a small sun, and a single carrier gear with two...
- Rohloff SpeedhubRohloff SpeedhubThe Rohloff Speedhub is an epicyclic internal hub gear for bicycles, developed and patented by Rohloff AG. It has been manufactured and marketed by the German company since 1998. The Speedhub 500/14 has 14 equally-spaced sequential gears with no overlapping ratios and is operated by a single...
, 14-ratio bicycle hub gearbox - Antikythera mechanismAntikythera mechanismThe Antikythera mechanism is an ancient mechanical computer designed to calculate astronomical positions. It was recovered in 1900–1901 from the Antikythera wreck. Its significance and complexity were not understood until decades later. Its time of construction is now estimated between 150 and 100...
, ancient mechanical astronomical computer
External links
- Parvalux have an animated 3D movie on their homepage of a 2-stage planetary gearhead in motion
- Kinematic Models for Design Digital Library (KMODDL)
Movies and photos of hundreds of working mechanical-systems models at Cornell. - "Animation of Epicyclic gearing"
- The "Power Split Device"
- The "Interactive Planetary Gearset tutorial"
- Interactive Prius planetary gear example" another one
- http://www.sciencedirect.com/science/article/pii/S0094114X09001578 Purely rotational model and vibration modes of compound planetary gears
- http://www.sciencedirect.com/science/article/pii/S0094114X01000337 Free torsional vibration characteristics of compound planetary gear sets
- http://link.aip.org/link/?JVACEK/129/1/1 Structured Vibration Modes of General Compound Planetary Gear Systems
- http://link.aip.org/link/?JVACEK/132/011006/1 Sensitivity of General Compound Planetary Gear Natural Frequencies and Vibration Modes to Model Parameters
- http://www.sciencedirect.com/science/article/pii/S0094114X11001443 Analytical determination of mesh phase relations in general compound planetary gears
- http://etd.ohiolink.edu/view.cgi?acc_num=osu1312289370 Ph.D. Dissertation on Compound Planetary Gears

