
Ensemble learning
Encyclopedia
In statistics
and machine learning
, ensemble methods use multiple models to obtain better predictive performance
than could be obtained from any of the constituent models.
Unlike a statistical ensemble in statistical mechanics, which is usually infinite, a machine learning ensemble refers only to a concrete finite set of alternative models.
algorithms are commonly described as performing the task of searching through a hypothesis space to find a suitable hypothesis that will make good predictions with a particular problem. Even if the hypothesis space contains hypotheses that are very well-suited for a particular problem, it may be very difficult to find a good one. Ensembles combine multiple hypotheses to form a (hopefully) better hypothesis. In other words, an ensemble is a technique for combining many weak learners in an attempt to produce a strong learner.
Evaluating the prediction of an ensemble typically requires more computation than evaluating the prediction of a single model, so ensembles may be thought of as a way to compensate for poor learning algorithms by performing a lot of extra computation. Fast algorithms such as decision trees
are commonly used with ensembles, although slower algorithms can benefit from ensemble techniques as well.
) tend to reduce problems related to over-fitting of the training data.
Empirically, ensembles tend to yield better results when there is a significant diversity among the models
. Many ensemble methods, therefore, seek to promote diversity among the models they combine. Although perhaps non-intuitive, more random algorithms (like random decision trees) can be used to produce a stronger ensemble than very deliberate algorithms (like entropy-reducing decision trees). Using a variety of strong learning algorithms, however, has been shown to be more effective than using techniques that attempt to dumb-down the models in order to promote diversity.
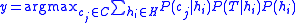
where is the predicted class,
is the predicted class,  is the set of all possible classes,
is the set of all possible classes,  is the hypothesis space,
is the hypothesis space,  refers to a probability, and
refers to a probability, and  is the training data. As an ensemble, the Bayes Optimal Classifier represents a hypothesis that is not necessarily in
is the training data. As an ensemble, the Bayes Optimal Classifier represents a hypothesis that is not necessarily in  . The hypothesis represented by the Bayes Optimal Classifier, however, is the optimal hypothesis in ensemble space (the space of all possible ensembles consisting only of hypotheses in
. The hypothesis represented by the Bayes Optimal Classifier, however, is the optimal hypothesis in ensemble space (the space of all possible ensembles consisting only of hypotheses in  ).
).
Unfortunately, Bayes Optimal Classifier cannot be practically implemented for any but the most simple of problems. There are several reasons why the Bayes Optimal Classifier cannot be practically implemented:
algorithm combines random decision trees with bagging to achieve very high classification accuracy.
, although some newer algorithms are reported to achieve better results.
may be used to draw hypotheses that are representative of the distribution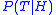 . It has been shown that under certain circumstances, when hypotheses are drawn in this manner and averaged according to Bayes' law, this technique has an expected error that is bounded to be at most twice the expected error of the Bayes optimal classifier . Despite the theoretical correctness of this technique, however, it has a tendency to promote over-fitting, and does not perform as well empirically as simpler ensemble techniques such as bagging.
. It has been shown that under certain circumstances, when hypotheses are drawn in this manner and averaged according to Bayes' law, this technique has an expected error that is bounded to be at most twice the expected error of the Bayes optimal classifier . Despite the theoretical correctness of this technique, however, it has a tendency to promote over-fitting, and does not perform as well empirically as simpler ensemble techniques such as bagging.
The use of Bayes' law to compute model weights necessitates computing the probability of the data given each model. Typically, none of the models in the ensemble are exactly the distribution from which the training data was generated, so all of them correctly receive a value close to zero for this term. This would work well if the ensemble were big enough to sample the entire model-space, but such is rarely possible. Consequently, each pattern in the training data will cause the ensemble weight to shift toward the model in the ensemble that is closest to the distribution of the training data. It essentially reduces to an unnecessarily complex method for doing performing selection.
The possible weightings for an ensemble can be visualized as lying on a simplex. At each vertex of the simplex, all of the weight is given to a single model in the ensemble. BMA converges toward the vertex that is closest to the distribution of the training data. By contrast, BMC converges toward the point where this distribution projects onto the simplex. In other words, instead of selecting the one model that is closest to the generating distribution, it seeks the combination of models that is closest to the generating distribution.
The results from BMA can often be approximated by using cross-validation to select the best model from a bucket of models. Likewise, the results from BMC may be approximated by using cross-validation to select the best ensemble combination from a random sampling of possible weightings.
The most common approach used for model-selection is cross-validation selection. It is described with the following pseudo-code:
For each model m in the bucket:
Do c times: (where 'c' is some constant)
Randomly divide the training dataset into two datasets: A, and B.
Train m with A
Test m with B
Select the model that obtains the highest average score
Cross-Validation Selection can be summed up as: "try them all with the training set, and pick the one that works best".
Gating is a generalization of Cross-Validation Selection. It involves training another learning model to decide which of the models in the bucket is best-suited to solve the problem. Often, a perceptron
is used for the gating model. It can be used to pick the "best" model, or it can be used to give a linear weight to the predictions from each model in the bucket.
When a bucket of models is used with a large set of problems, it may be desirable to avoid training some of the models that take a long time to train. Landmark learning is a meta-learning approach that seeks to solve this problem. It involves training only the fast (but imprecise) algorithms in the bucket, and then using the performance of these algorithms to help determine which slow (but accurate) algorithm is most likely to do best.
judge among a set of models by comparing them on data that was not used
to create any of them. This same prior belief underlies the use in machine learning of
bake-off contests to judge which of a set of
competitor learning algorithms is actually best.
This prior belief can also be used
by a single practitioner, to choose among a set of models based on
a single data set. This is done by partitioning the data set into a
held-in data set and a held-out data set; training the models
on the held-in data; and then choosing whichever of those
trained models performs best on the held-out data. This is the
cross-validation technique, mentioned above.
Stacking (sometimes called stacked generalization) exploits this prior belief further.
It does this by using performance on
the held-out data to combine the models rather than choose among
them, thereby typically getting performance better than any single one of the
trained models..
It has been successfully used on both supervised learning tasks
(regression)
and unsupervised learning (density estimation). It has also been used to
estimate Bagging's error rate.
Because the prior belief concerning
held-out data is so powerful, stacking often out-performs
Bayesian model-averaging.
Indeed, renamed blending, stacking was extensively used in the two
top performers in the recent Netflix
competition.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, ensemble methods use multiple models to obtain better predictive performance
Predictive inference
Predictive inference is an approach to statistical inference that emphasizes the prediction of future observations based on past observations.Initially, predictive inference was based on observable parameters and it was the main purpose of studying probability, but it fell out of favor in the 20th...
than could be obtained from any of the constituent models.
Unlike a statistical ensemble in statistical mechanics, which is usually infinite, a machine learning ensemble refers only to a concrete finite set of alternative models.
Overview
Supervised learningSupervised learning
Supervised learning is the machine learning task of inferring a function from supervised training data. The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value...
algorithms are commonly described as performing the task of searching through a hypothesis space to find a suitable hypothesis that will make good predictions with a particular problem. Even if the hypothesis space contains hypotheses that are very well-suited for a particular problem, it may be very difficult to find a good one. Ensembles combine multiple hypotheses to form a (hopefully) better hypothesis. In other words, an ensemble is a technique for combining many weak learners in an attempt to produce a strong learner.
Evaluating the prediction of an ensemble typically requires more computation than evaluating the prediction of a single model, so ensembles may be thought of as a way to compensate for poor learning algorithms by performing a lot of extra computation. Fast algorithms such as decision trees
Decision tree learning
Decision tree learning, used in statistics, data mining and machine learning, uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. More descriptive names for such tree models are classification trees or regression trees...
are commonly used with ensembles, although slower algorithms can benefit from ensemble techniques as well.
Ensemble theory
An ensemble is itself a supervised learning algorithm, because it can be trained and then used to make predictions. The trained ensemble, therefore, represents a single hypothesis. This hypothesis, however, is not necessarily contained within the hypothesis space of the models from which it is built. Thus, ensembles can be shown to have more flexibility in the functions they can represent. This flexibility can, in theory, enable them to over-fit the training data more than a single model would, but in practice, some ensemble techniques (especially baggingBootstrap aggregating
Bootstrap aggregating is a machine learning ensemble meta-algorithm to improve machine learning of statistical classification and regression models in terms of stability and classification accuracy. It also reduces variance and helps to avoid overfitting. Although it is usually applied to decision...
) tend to reduce problems related to over-fitting of the training data.
Empirically, ensembles tend to yield better results when there is a significant diversity among the models
. Many ensemble methods, therefore, seek to promote diversity among the models they combine. Although perhaps non-intuitive, more random algorithms (like random decision trees) can be used to produce a stronger ensemble than very deliberate algorithms (like entropy-reducing decision trees). Using a variety of strong learning algorithms, however, has been shown to be more effective than using techniques that attempt to dumb-down the models in order to promote diversity.
Bayes optimal classifier
The Bayes Optimal Classifier is an optimal classification technique. It is an ensemble of all the hypotheses in the hypothesis space. On average, no other ensemble can outperform it, so it is the ideal ensemble. Each hypothesis is given a vote proportional to the likelihood that the training dataset would be sampled from a system if that hypothesis were true. To facilitate training data of finite size, the vote of each hypothesis is also multiplied by the prior probability of that hypothesis. The Bayes Optimal Classifier can be expressed with following equation: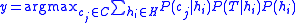
where
 is the predicted class,
is the predicted class,  is the set of all possible classes,
is the set of all possible classes,  is the hypothesis space,
is the hypothesis space,  refers to a probability, and
refers to a probability, and  is the training data. As an ensemble, the Bayes Optimal Classifier represents a hypothesis that is not necessarily in
is the training data. As an ensemble, the Bayes Optimal Classifier represents a hypothesis that is not necessarily in  . The hypothesis represented by the Bayes Optimal Classifier, however, is the optimal hypothesis in ensemble space (the space of all possible ensembles consisting only of hypotheses in
. The hypothesis represented by the Bayes Optimal Classifier, however, is the optimal hypothesis in ensemble space (the space of all possible ensembles consisting only of hypotheses in  ).
).Unfortunately, Bayes Optimal Classifier cannot be practically implemented for any but the most simple of problems. There are several reasons why the Bayes Optimal Classifier cannot be practically implemented:
- Most interesting hypothesis spaces are too large to iterate over, as required by the
 .
. - Many hypotheses yield only a predicted class, rather than a probability for each class as required by the term
 .
. - Computing an unbiased estimate of the probability of the training set given a hypothesis (
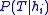 ) is non-trivial.
) is non-trivial. - Estimating the prior probability for each hypothesis (
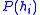 ) is rarely feasible.
) is rarely feasible.
Bootstrap aggregating (bagging)
Bootstrap aggregating, often abbreviated as bagging, involves having each model in the ensemble vote with equal weight. In order to promote model variance, bagging trains each model in the ensemble using a randomly-drawn subset of the training set. As an example, the random forestRandom forest
Random forest is an ensemble classifier that consists of many decision trees and outputs the class that is the mode of the class's output by individual trees. The algorithm for inducing a random forest was developed by Leo Breiman and Adele Cutler, and "Random Forests" is their trademark...
algorithm combines random decision trees with bagging to achieve very high classification accuracy.
Boosting
Boosting involves incrementally building an ensemble by training each new model instance to emphasize the training instances that previous models mis-classified. In some cases, boosting has been shown to yield better accuracy than bagging, but it also tends to be more likely to over-fit the training data. By far, the most common implementation of Boosting is AdaboostAdaBoost
AdaBoost, short for Adaptive Boosting, is a machine learning algorithm, formulated by Yoav Freund and Robert Schapire. It is a meta-algorithm, and can be used in conjunction with many other learning algorithms to improve their performance. AdaBoost is adaptive in the sense that subsequent...
, although some newer algorithms are reported to achieve better results.
Bayesian model averaging
Bayesian model averaging is an ensemble technique that seeks to approximate the Bayes Optimal Classifier by sampling hypotheses from the hypothesis space, and combining them using Bayes' law. Unlike the Bayes optimal classifier, Bayesian model averaging can be practically implemented. Hypotheses are typically sampled using a Monte Carlo sampling technique such as MCMC. For example, Gibbs samplingGibbs sampling
In statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is an algorithm to generate a sequence of samples from the joint probability distribution of two or more random variables...
may be used to draw hypotheses that are representative of the distribution
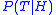 . It has been shown that under certain circumstances, when hypotheses are drawn in this manner and averaged according to Bayes' law, this technique has an expected error that is bounded to be at most twice the expected error of the Bayes optimal classifier . Despite the theoretical correctness of this technique, however, it has a tendency to promote over-fitting, and does not perform as well empirically as simpler ensemble techniques such as bagging.
. It has been shown that under certain circumstances, when hypotheses are drawn in this manner and averaged according to Bayes' law, this technique has an expected error that is bounded to be at most twice the expected error of the Bayes optimal classifier . Despite the theoretical correctness of this technique, however, it has a tendency to promote over-fitting, and does not perform as well empirically as simpler ensemble techniques such as bagging.Pseudo-code
function train_bayesian_model_averaging(T)
z = -infinity
For each model, m, in the ensemble:
Train m, typically using a random subset of the training data, T.
Let prior[m] be the prior probability that m is the generating hypothesis.
Typically, uniform priors are used, so prior[m] = 1.
Let x be the predictive accuracy (from 0 to 1) of m for predicting the labels in T.
Use x to estimate log_likelihood[m]. Often, this is computed as
log_likelihood[m] = |T| * (x * log(x) + (1 - x) * log(1 - x)),
where |T| is the number of training patterns in T.
z = max(z, log_likelihood[m])
For each model, m, in the ensemble:
weight[m] = prior[m] * exp(log_likelihood[m] - z)
Normalize all the model weights to sum to 1.
Bayesian model combination
Bayesian model combination (BMC) is an algorithmic correction to BMA. Instead of sampling each model in the ensemble individually, it samples from the space of possible ensembles (with model weightings drawn randomly from a Dirichlet distribution having uniform parameters). This modification overcomes the tendency of BMA to converge toward giving all of the weight to a single model. Although BMC is somewhat more computationally expensive than BMA, it tends to yield dramatically better results. The results from BMC have been shown to be better on average (with statistical significance) than BMA, and bagging.The use of Bayes' law to compute model weights necessitates computing the probability of the data given each model. Typically, none of the models in the ensemble are exactly the distribution from which the training data was generated, so all of them correctly receive a value close to zero for this term. This would work well if the ensemble were big enough to sample the entire model-space, but such is rarely possible. Consequently, each pattern in the training data will cause the ensemble weight to shift toward the model in the ensemble that is closest to the distribution of the training data. It essentially reduces to an unnecessarily complex method for doing performing selection.
The possible weightings for an ensemble can be visualized as lying on a simplex. At each vertex of the simplex, all of the weight is given to a single model in the ensemble. BMA converges toward the vertex that is closest to the distribution of the training data. By contrast, BMC converges toward the point where this distribution projects onto the simplex. In other words, instead of selecting the one model that is closest to the generating distribution, it seeks the combination of models that is closest to the generating distribution.
The results from BMA can often be approximated by using cross-validation to select the best model from a bucket of models. Likewise, the results from BMC may be approximated by using cross-validation to select the best ensemble combination from a random sampling of possible weightings.
Pseudo-code
function train_bayesian_model_combination(T)
{
For each model, m, in the ensemble:
weight[m] = 0
sum_weight = 0
z = -infinity
Let n be some number of weightings to sample.
(100 might be a reasonable value. Smaller is faster. Bigger leads to more precise results.)
for i from 0 to n - 1:
For each model, m, in the ensemble: // draw from a uniform Dirichlet distribution
v[m] = -log(random_uniform(0,1))
Normalize v to sum to 1
Let x be the predictive accuracy (from 0 to 1) of the entire ensemble, weighted
according to v, for predicting the labels in T.
Use x to estimate log_likelihood[i]. Often, this is computed as
log_likelihood[i] = |T| * (x * log(x) + (1 - x) * log(1 - x)),
where |T| is the number of training patterns in T.
If log_likelihood[i] > z: // z is used to maintain numerical stability
For each model, m, in the ensemble:
weight[m] = weight[m] * exp(z - log_likelihood[i])
z = log_likelihood[i]
w = exp(log_likelihood[i] - z)
For each model, m, in the ensemble:
weight[m] = weight[m] * sum_weight / (sum_weight + w) + w * v[m]
sum_weight = sum_weight + w
Normalize the model weights to sum to 1.
}
Bucket of models
A "bucket of models" is an ensemble in which a model selection algorithm is used to choose the best model for each problem. When tested with only one problem, a bucket of models can produce no better results than the best model in the set, but when evaluated across many problems, it will typically produce much better results, on average, than any model in the set.The most common approach used for model-selection is cross-validation selection. It is described with the following pseudo-code:
For each model m in the bucket:
Do c times: (where 'c' is some constant)
Randomly divide the training dataset into two datasets: A, and B.
Train m with A
Test m with B
Select the model that obtains the highest average score
Cross-Validation Selection can be summed up as: "try them all with the training set, and pick the one that works best".
Gating is a generalization of Cross-Validation Selection. It involves training another learning model to decide which of the models in the bucket is best-suited to solve the problem. Often, a perceptron
Perceptron
The perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
is used for the gating model. It can be used to pick the "best" model, or it can be used to give a linear weight to the predictions from each model in the bucket.
When a bucket of models is used with a large set of problems, it may be desirable to avoid training some of the models that take a long time to train. Landmark learning is a meta-learning approach that seeks to solve this problem. It involves training only the fast (but imprecise) algorithms in the bucket, and then using the performance of these algorithms to help determine which slow (but accurate) algorithm is most likely to do best.
Stacking
The crucial prior belief underlying the scientific method is that one canjudge among a set of models by comparing them on data that was not used
to create any of them. This same prior belief underlies the use in machine learning of
bake-off contests to judge which of a set of
competitor learning algorithms is actually best.
This prior belief can also be used
by a single practitioner, to choose among a set of models based on
a single data set. This is done by partitioning the data set into a
held-in data set and a held-out data set; training the models
on the held-in data; and then choosing whichever of those
trained models performs best on the held-out data. This is the
cross-validation technique, mentioned above.
Stacking (sometimes called stacked generalization) exploits this prior belief further.
It does this by using performance on
the held-out data to combine the models rather than choose among
them, thereby typically getting performance better than any single one of the
trained models..
It has been successfully used on both supervised learning tasks
(regression)
and unsupervised learning (density estimation). It has also been used to
estimate Bagging's error rate.
Because the prior belief concerning
held-out data is so powerful, stacking often out-performs
Bayesian model-averaging.
Indeed, renamed blending, stacking was extensively used in the two
top performers in the recent Netflix
competition.

