
Ensemble Interpretation
Encyclopedia
The ensemble interpretation, or statistical interpretation of quantum mechanics
, is an interpretation that can be viewed as a minimalist interpretation; it is a quantum mechanical interpretation that claims to make the fewest assumptions associated with the standard mathematical formalization. At its heart, it takes to the fullest extent the statistical
interpretation of Max Born
for which he won Nobel Prize in Physics
. The interpretation states that the wave function
does not apply to an individual system – or for example, a single particle – but is an abstract mathematical, statistical quantity that only applies to an ensemble of similarly prepared systems or particles. Probably the most notable supporter of such an interpretation was Albert Einstein
:
To date, probably the most prominent advocate of the ensemble interpretation is Leslie E. Ballentine, Professor at Simon Fraser University
, and writer of the graduate-level textbook "Quantum Mechanics, A Modern Development".
The ensemble interpretation, unlike many other interpretations of quantum mechanics, does not attempt to justify, or otherwise derive, or explain quantum mechanics from any deterministic process, or make any other statement about the real nature of quantum phenomena; it is simply a statement as to the manner of wave function interpretation.
states, and other issues related to the concepts of multiple simultaneous states. As the ensemble interpretation postulates that the wave function only applies to an ensemble of systems, there is no requirement for any single system to exist in more than one state at a time, hence, the wave function is never physically required to be "reduced". This can be illustrated by an example:
Consider a classical die. If this is expressed in Dirac notation
, the "state" of the die can be represented by a "wave" function describing the probability of an outcome given by:
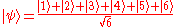
It is clear that on each throw, only one of the states will be observed, but it is also clear that there is no requirement for any notion of collapse of the wave function/reduction of the state vector, or for the die to physically exist in the summed state. In the ensemble interpretation, wave function collapse would make as much sense as saying that the number of children a couple produced, collapsed to 3 from its average value of 2.4.
The state function is not taken to be physically real, or be a literal summation of states. The wave function, is taken to be an abstract statistical function, only applicable to the statistics of repeated preparation procedures, similar to classical statistical mechanics
. It does not directly apply to a single experiment, only the statistical results of many.
He also emphasises the importance of describing single systems, rather than ensembles.
It can also be argued that this notion is consistent with the standard interpretation in that, in the Copenhagen interpretation, statements about the exact system state prior to measurement can not be made. That is, if it were possible to absolutely, physically measure say, a particle in two positions at once, then quantum mechanics would be falsified as quantum mechanics explicitly postulates that the result of any measurement must be a single eigenvalue of a single eigenstate.
paradox a trivial non-issue. However, the application of state vectors to individual systems, rather than ensembles, has explanatory benefits, in areas like single-particle twin-slit experiments and quantum computing (see Schrödinger's cat applications). As an avowedly minimalist approach, the ensemble interpretation does not offer any specific alternative explanation for these phenomena.
or stochastic
theory.
Probability always require a set of multiple data, and thus single-particle experiments are
really part of an ensemble — an ensemble of individual experiments that are performed one after the other over time. In particular, the interference fringes seen in the double-slit experiment
require repeated trials to be observed.
that, under certain circumstances, a repeatedly measured system, such as an unstable nucleus, would be prevented from decaying by the act of measurement itself. He initially presented this as a kind of reductio ad absurdum
of wave function collapse.
The effect has been shown to be real. (It is more widely known as the quantum Zeno effect
). Ballentine later wrote papers claiming that it could be explained without wave function collapse.
a classical theory. John Gribbin
writes:
However, hopes for turning quantum mechanics back into a classical theory were dashed. Gribbin continues:
Willem de Muynck describes an "objective-realist" version of the ensemble interpretation featuring counterfactual definiteness
and the "possessed values principle", in which values of the quantum mechanical observables may be attributed to the object as objective properties the object possesses independent of observation. He states that
there are "strong indications, if not proofs" that neither is a possible assumption.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, is an interpretation that can be viewed as a minimalist interpretation; it is a quantum mechanical interpretation that claims to make the fewest assumptions associated with the standard mathematical formalization. At its heart, it takes to the fullest extent the statistical
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
interpretation of Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
for which he won Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
. The interpretation states that the wave function
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
does not apply to an individual system – or for example, a single particle – but is an abstract mathematical, statistical quantity that only applies to an ensemble of similarly prepared systems or particles. Probably the most notable supporter of such an interpretation was Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
:
To date, probably the most prominent advocate of the ensemble interpretation is Leslie E. Ballentine, Professor at Simon Fraser University
Simon Fraser University
Simon Fraser University is a Canadian public research university in British Columbia with its main campus on Burnaby Mountain in Burnaby, and satellite campuses in Vancouver and Surrey. The main campus in Burnaby, located from downtown Vancouver, was established in 1965 and has more than 34,000...
, and writer of the graduate-level textbook "Quantum Mechanics, A Modern Development".
The ensemble interpretation, unlike many other interpretations of quantum mechanics, does not attempt to justify, or otherwise derive, or explain quantum mechanics from any deterministic process, or make any other statement about the real nature of quantum phenomena; it is simply a statement as to the manner of wave function interpretation.
Measurement and collapse
The attraction of the ensemble interpretation is that it immediately dispenses with the metaphysical issues associated with reduction of the state vector, Schrödinger catSchrödinger's cat
Schrödinger's cat is a thought experiment, usually described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The scenario presents a cat that might be...
states, and other issues related to the concepts of multiple simultaneous states. As the ensemble interpretation postulates that the wave function only applies to an ensemble of systems, there is no requirement for any single system to exist in more than one state at a time, hence, the wave function is never physically required to be "reduced". This can be illustrated by an example:
Consider a classical die. If this is expressed in Dirac notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
, the "state" of the die can be represented by a "wave" function describing the probability of an outcome given by:
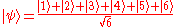
It is clear that on each throw, only one of the states will be observed, but it is also clear that there is no requirement for any notion of collapse of the wave function/reduction of the state vector, or for the die to physically exist in the summed state. In the ensemble interpretation, wave function collapse would make as much sense as saying that the number of children a couple produced, collapsed to 3 from its average value of 2.4.
The state function is not taken to be physically real, or be a literal summation of states. The wave function, is taken to be an abstract statistical function, only applicable to the statistics of repeated preparation procedures, similar to classical statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. It does not directly apply to a single experiment, only the statistical results of many.
Criticism
David Mermin sees the Ensemble interpretation as being motivated by an adherence ("not always acknowledged") to classical principles."For the notion that probabilistic theories must
be about ensembles implicitly assumes that probability is about ignorance. (The 'hidden
variables' are whatever it is that we are ignorant of.) But in a non-deterministic world
probability has nothing to do with incomplete knowledge, and ought not to require an
ensemble of systems for its interpretation".
He also emphasises the importance of describing single systems, rather than ensembles.
"The second motivation for an ensemble interpretation is the intuition that because
quantum mechanics is inherently probabilistic, it only needs to make sense as a theory of
ensembles. Whether or not probabilities can be given a sensible meaning for individual
systems, this motivation is not compelling. For a theory ought to be able to describe as
well as predict the behavior of the world. The fact that physics cannot make deterministic
predictions about individual systems does not excuse us from pursuing the goal of being
able to describe them as they currently are."
Single particles
According to proponents of this interpretation, no single system is ever required to be postulated to exist in a physical mixed state so the state vector does not need to collapse.It can also be argued that this notion is consistent with the standard interpretation in that, in the Copenhagen interpretation, statements about the exact system state prior to measurement can not be made. That is, if it were possible to absolutely, physically measure say, a particle in two positions at once, then quantum mechanics would be falsified as quantum mechanics explicitly postulates that the result of any measurement must be a single eigenvalue of a single eigenstate.
Criticism
Arnold Neumaier finds limitations with the applicability of the ensemble interpretation to small systems.
"Among the traditional interpretations, the statistical interpretation
discussed by Ballentine in Rev. Mod. Phys. 42, 358-381 (1970) is the
least demanding (assumes less than the Copenhagen interpretation
and the Many Worlds interpretation) and the most consistent one.
It explains almost everything, and only has the disadvantage that
it explicitly excludes the applicability of QM to single systems or very small ensembles (such as the few solar neutrinos or top quarks
actually detected so far), and does not bridge the gulf between
the classical domain (for the description of detectors) and the
quantum domain (for the description of the microscopic system)".
(spelling amended)
Schrödinger's cat
The ensemble interpretation states that superpositions are nothing but subensembles of a larger statistical ensemble. That being the case, the state vector would not apply to individual cat experiments, but only to the statistics of many similar prepared cat experiments. Proponents of this interpretation state that this makes the Schrödinger's catSchrödinger's cat
Schrödinger's cat is a thought experiment, usually described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The scenario presents a cat that might be...
paradox a trivial non-issue. However, the application of state vectors to individual systems, rather than ensembles, has explanatory benefits, in areas like single-particle twin-slit experiments and quantum computing (see Schrödinger's cat applications). As an avowedly minimalist approach, the ensemble interpretation does not offer any specific alternative explanation for these phenomena.
The frequentist probability variation
The claim that the wave functional approach fails to apply to single particle experiments cannot be taken as a claim that quantum mechanics fails in describing single-particle phenomena. In fact, it gives correct results within the limits of a probabilisticProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
or stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
theory.
Probability always require a set of multiple data, and thus single-particle experiments are
really part of an ensemble — an ensemble of individual experiments that are performed one after the other over time. In particular, the interference fringes seen in the double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
require repeated trials to be observed.
The quantum Zeno effect
Leslie Ballantine promoted the ensemble interpretation in his book Quantum Mechanics, A Modern Development. In it, he described what he called the "Watched Pot Experiment". His argument wasthat, under certain circumstances, a repeatedly measured system, such as an unstable nucleus, would be prevented from decaying by the act of measurement itself. He initially presented this as a kind of reductio ad absurdum
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
of wave function collapse.
The effect has been shown to be real. (It is more widely known as the quantum Zeno effect
Quantum Zeno effect
The quantum Zeno effect is a name coined by George Sudarshan and Baidyanath Misra of the University of Texas in 1977 in their analysis of the situation in which an unstable particle, if observed continuously, will never decay. One can nearly "freeze" the evolution of the system by measuring it...
). Ballentine later wrote papers claiming that it could be explained without wave function collapse.
Earlier Classical Ensemble Ideas
Early proponents of statistical approaches regarded quantum mechanics as an approximation toa classical theory. John Gribbin
John Gribbin
John R. Gribbin is a British science writer and a visiting Fellow in astronomy at the University of Sussex.- Biography :John Gribbin graduated with his bachelor's degree in physics from the University of Sussex in 1966. Gribbin then earned his master of science degree in astronomy in 1967, also...
writes:
"The basic idea is that each quantum entity (such as an electron or a photon) has precise quantum properties (such as position or momentum) and the quantum wavefunction is related to the probability of getting a particular experimental result when one member (or many members) of the ensemble is selected by an experiment"
However, hopes for turning quantum mechanics back into a classical theory were dashed. Gribbin continues:
"There are many difficulties with the idea, but the killer blow was struck when individual quantum entities such as photons were observed behaving in experiments in line with the quantum wave function description. The Ensemble interpretation is now only of historical interest."
Willem de Muynck describes an "objective-realist" version of the ensemble interpretation featuring counterfactual definiteness
Counterfactual definiteness
In some interpretations of quantum mechanics, counterfactual definiteness is the ability to speak with meaning of the definiteness of the results of measurements that have not been performed...
and the "possessed values principle", in which values of the quantum mechanical observables may be attributed to the object as objective properties the object possesses independent of observation. He states that
there are "strong indications, if not proofs" that neither is a possible assumption.
External links
- Quantum mechanics as Wim Muynk sees it
- Einstein's reply to criticisms
- Kevin Aylwards's account of the ensemble interpretation
- Detailed ensemble interpretation by Marcel Nooijen
- Pechenkin, A.A. The early statistical interpretations of quantum mechanics
- Krüger, T. An attempt to close the Einstein–Podolsky–Rosen debate
- Duda, J. Four-dimensional understanding of quantum mechanics

