
End extension
Encyclopedia
In model theory
and set theory
, which are disciplines within mathematics, a model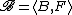 of some axiom system of set theory
of some axiom system of set theory
 in the language of set theory is an end extension of
in the language of set theory is an end extension of 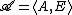 , in symbols
, in symbols 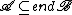 , if
, if
The following is an equivalent definition of end extension: is a substructure
is a substructure
of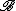 , and
, and 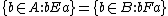 for all
for all 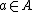 .
.
For example,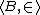 is an end extension of
is an end extension of 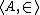 if
if 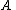 and
and 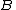 are transitive set
are transitive set
s, and .
.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
and set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, which are disciplines within mathematics, a model
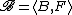 of some axiom system of set theory
of some axiom system of set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
 in the language of set theory is an end extension of
in the language of set theory is an end extension of 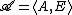 , in symbols
, in symbols 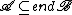 , if
, if
-
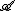 is a substructureSubstructureIn mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
is a substructureSubstructureIn mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
of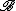 , and
, and -
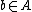 whenever
whenever  and
and 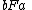 hold, i.e., no new elements are added by
hold, i.e., no new elements are added by 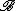 to the elements of
to the elements of 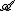 .
.
The following is an equivalent definition of end extension:
 is a substructure
is a substructureSubstructure
In mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
of
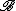 , and
, and 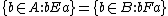 for all
for all 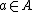 .
.For example,
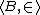 is an end extension of
is an end extension of 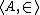 if
if 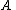 and
and 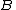 are transitive set
are transitive setTransitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
s, and
 .
.

