
Embedded pushdown automaton
Encyclopedia
An embedded pushdown automaton or EPDA is a computational model
for parsing languages generated by tree-adjoining grammar
s (TAGs). It is similar to the context-free grammar
-parsing pushdown automaton
, except that instead of using a plain stack
to store symbols, it has a stack of iterated stacks that store symbols, giving TAGs a generative capacity between context-free grammars and context-sensitive grammar
s, or a subset of the mildly context-sensitive grammars.
to this class. Various subgrammars, such as the linear indexed grammar, can thus be defined. They are also beginning to play an important role in natural language processing.
While natural languages have traditionally been analyzed using context-free grammars (see transformational-generative grammar and computational linguistics
), this model does not work well for languages with crossed dependencies, such as Dutch, situations for which an EPDA is well suited. A detailed linguistic analysis is available in .
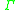 , and so we define an element of a stack by
, and so we define an element of a stack by 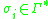 , where the star is the Kleene closure of the alphabet.
, where the star is the Kleene closure of the alphabet.
Each stack can then be defined in terms of its elements, so we denote the th stack in the automaton using a double-dagger symbol:
th stack in the automaton using a double-dagger symbol: 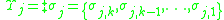 , where
, where  would be the next accessible symbol in the stack. The embedded stack of
would be the next accessible symbol in the stack. The embedded stack of  stacks can thus be denoted by
stacks can thus be denoted by  .
.
We define an EPDA by the septuple (7-tuple)
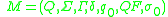 where
where
Thus the transition function takes a state, the next symbol of the input string, and the top symbol of the current stack and generates the next state, the stacks to be pushed and popped onto the embedded stack, the pushing and popping of the current stack, and the stacks to be considered the current stacks in the next transition. More conceptually, the embedded stack is pushed and popped, the current stack is optionally pushed back onto the embedded stack, and any other stacks one would like are pushed on top of that, with the last stack being the one read from in the next iteration. Therefore, stacks can be pushed both above and below the current stack.
A given configuration is defined by
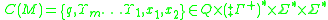
where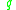 is the current state, the
is the current state, the 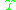 s are the stacks in the embedded stack, with
s are the stacks in the embedded stack, with 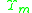 the current stack, and for an input string
the current stack, and for an input string 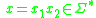 ,
, 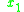 is the portion of the string already processed by the machine and
is the portion of the string already processed by the machine and 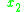 is the portion to be processed, with its head being the current symbol read. Note that the empty string
is the portion to be processed, with its head being the current symbol read. Note that the empty string  is implicitly defined as a terminating symbol, where if the machine is at a final state when the empty string is read, the entire input string is accepted, and if not it is rejected. Such accepted strings are elements of the language
is implicitly defined as a terminating symbol, where if the machine is at a final state when the empty string is read, the entire input string is accepted, and if not it is rejected. Such accepted strings are elements of the language
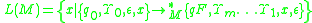
where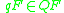 and
and 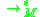 defines the transition function applied over as many times as necessary to parse the string.
defines the transition function applied over as many times as necessary to parse the string.
Computational model
A computational model is a mathematical model in computational science that requires extensive computational resources to study the behavior of a complex system by computer simulation. The system under study is often a complex nonlinear system for which simple, intuitive analytical solutions are...
for parsing languages generated by tree-adjoining grammar
Tree-adjoining grammar
Tree-adjoining grammar is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol...
s (TAGs). It is similar to the context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
-parsing pushdown automaton
Pushdown automaton
In automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
, except that instead of using a plain stack
Stack (data structure)
In computer science, a stack is a last in, first out abstract data type and linear data structure. A stack can have any abstract data type as an element, but is characterized by only three fundamental operations: push, pop and stack top. The push operation adds a new item to the top of the stack,...
to store symbols, it has a stack of iterated stacks that store symbols, giving TAGs a generative capacity between context-free grammars and context-sensitive grammar
Context-sensitive grammar
A context-sensitive grammar is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols...
s, or a subset of the mildly context-sensitive grammars.
History and applications
EPDAs were first described by K. Vijay-Shanker in his 1988 doctoral thesis. They have since been applied to more complete descriptions of the class of mildly context-sensitive grammars and have had important roles in extending and refining the Chomsky hierarchyChomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
to this class. Various subgrammars, such as the linear indexed grammar, can thus be defined. They are also beginning to play an important role in natural language processing.
While natural languages have traditionally been analyzed using context-free grammars (see transformational-generative grammar and computational linguistics
Computational linguistics
Computational linguistics is an interdisciplinary field dealing with the statistical or rule-based modeling of natural language from a computational perspective....
), this model does not work well for languages with crossed dependencies, such as Dutch, situations for which an EPDA is well suited. A detailed linguistic analysis is available in .
Theory
An EPDA is a finite state machine with a set of stacks that can be themselves accessed through the embedded stack. Each stack contains elements of the stack alphabet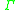 , and so we define an element of a stack by
, and so we define an element of a stack by 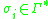 , where the star is the Kleene closure of the alphabet.
, where the star is the Kleene closure of the alphabet.Each stack can then be defined in terms of its elements, so we denote the
 th stack in the automaton using a double-dagger symbol:
th stack in the automaton using a double-dagger symbol: 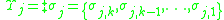 , where
, where  would be the next accessible symbol in the stack. The embedded stack of
would be the next accessible symbol in the stack. The embedded stack of  stacks can thus be denoted by
stacks can thus be denoted by  .
.We define an EPDA by the septuple (7-tuple)
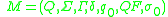 where
where-
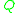 is a finite set of states;
is a finite set of states; -
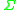 is the finite set of the input alphabet;
is the finite set of the input alphabet; -
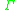 is the finite stack alphabet;
is the finite stack alphabet; -
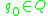 is the start state;
is the start state; -
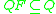 is the set of final states;
is the set of final states; -
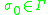 is the initial stack symbol
is the initial stack symbol -
 is the transition function, where
is the transition function, where 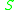 are finite subsets of
are finite subsets of 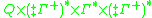 .
.
Thus the transition function takes a state, the next symbol of the input string, and the top symbol of the current stack and generates the next state, the stacks to be pushed and popped onto the embedded stack, the pushing and popping of the current stack, and the stacks to be considered the current stacks in the next transition. More conceptually, the embedded stack is pushed and popped, the current stack is optionally pushed back onto the embedded stack, and any other stacks one would like are pushed on top of that, with the last stack being the one read from in the next iteration. Therefore, stacks can be pushed both above and below the current stack.
A given configuration is defined by
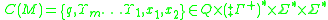
where
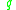 is the current state, the
is the current state, the 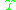 s are the stacks in the embedded stack, with
s are the stacks in the embedded stack, with 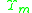 the current stack, and for an input string
the current stack, and for an input string 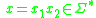 ,
, 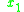 is the portion of the string already processed by the machine and
is the portion of the string already processed by the machine and 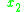 is the portion to be processed, with its head being the current symbol read. Note that the empty string
is the portion to be processed, with its head being the current symbol read. Note that the empty string  is implicitly defined as a terminating symbol, where if the machine is at a final state when the empty string is read, the entire input string is accepted, and if not it is rejected. Such accepted strings are elements of the language
is implicitly defined as a terminating symbol, where if the machine is at a final state when the empty string is read, the entire input string is accepted, and if not it is rejected. Such accepted strings are elements of the language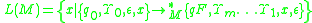
where
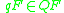 and
and 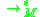 defines the transition function applied over as many times as necessary to parse the string.
defines the transition function applied over as many times as necessary to parse the string.

