
Elementary Calculus: An Infinitesimal Approach
Encyclopedia
Elementary Calculus: An Infinitesimal approach (the subtitle is sometimes given as An approach using infinitesimals) is a textbook by H. Jerome Keisler
. The subtitle alludes to the infinitesimal
numbers of Abraham Robinson
's non-standard analysis
. The book is available freely online and is currently published by Dover.
numbers. Because this is not a subject widely known Keisler also published a companion book, Foundations of Infinitesimal Calculus, for instructors which covers the foundational material in more depth.
In his textbook, Keisler used the pedagogical technique of an infinite-magnification microscope, so as to represent graphically, distinct hyperreal number
s infinitely close to each other.
When one examines a curve, say the graph of ƒ, under a magnifying glass, its curvature decreases proportionally to the magnification power of the lens. Similarly, an infinite-magnification microscope will transform an infinitesimal arc of a graph of ƒ, into a straight line, up to an infinitesimal error (only visible by applying a higher-magnification "microscope"). The derivative of ƒ is then the (standard part of the) slope of that line. Thus the microscope is used as a device in explaining the derivative.
In the second edition Keisler introduces the extension principle and the transfer principle in the following form:
Keisler then gives a few examples of real statements to which the principle applies:
Howard Jerome Keisler
H. Jerome Keisler is an American mathematician, currently professor emeritus at University of Wisconsin–Madison. His research has included model theory and non-standard analysis.His Ph.D...
. The subtitle alludes to the infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
numbers of Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
's non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
. The book is available freely online and is currently published by Dover.
Textbook
Keisler's textbook was based on Robinson's construction of the hyperrealHyperreal
Hyperreal may refer to:* Hyperreal numbers, an extension of the real numbers in mathematics that are used in non-standard analysis* Hyperreality, a term used in semiotics and postmodern philosophy* Hyperrealism, a school of painting...
numbers. Because this is not a subject widely known Keisler also published a companion book, Foundations of Infinitesimal Calculus, for instructors which covers the foundational material in more depth.
In his textbook, Keisler used the pedagogical technique of an infinite-magnification microscope, so as to represent graphically, distinct hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
s infinitely close to each other.
When one examines a curve, say the graph of ƒ, under a magnifying glass, its curvature decreases proportionally to the magnification power of the lens. Similarly, an infinite-magnification microscope will transform an infinitesimal arc of a graph of ƒ, into a straight line, up to an infinitesimal error (only visible by applying a higher-magnification "microscope"). The derivative of ƒ is then the (standard part of the) slope of that line. Thus the microscope is used as a device in explaining the derivative.
Reception
The book received both positive and negative reviews. Keisler's student K. Sullivan, as part of her Ph.D. thesis performed a controlled experiment involving 5 schools, which found Elementary Calculus to have advantages over the standard method of teaching calculus. Despite the benefits described by Sullivan, the vast majority of mathematicians were not convinced to adopt infinitesimal methods in their teaching. Recently, Katz & Katz give a positive account of a calculus course. O'Donovan also described his experience teaching calculus using infinitesimals. His initial point of view was positive , but later he found pedagogical difficulties with the approach. After discussing his difficulties with K. Hrbacek, Hrbacek identified the fundamental mathematical source of pedagogical difficulties O'Donovan faced. Hrbacek states that in order to define define basic notions from calculus such as continuity, differentiation and integration implicitly must be grounded in the ε-δ method in the Robinson framework. Thus the hope that non-standard calculus could be done without ε-δ methods could not be realized in full.. Both find infinitesimal techniques to be intuitive to students and a useful teaching tool, and together with Lessmann they put forth their own theory of relative analysis (sometimes called stratified analysis), which allow for infinitesimal techniques but possesses a more general transfer principle that maybe safely used by students.Transfer principle
Between the first and second edition of the Elementary Calculus, much of the theoretical material that was in the first chapter was moved to the epilogue at the end of the book. Including the theoretical groundwork of Non-standard analysis.In the second edition Keisler introduces the extension principle and the transfer principle in the following form:
- Every real statement that holds for one or more particular real functions holds for the hyperreal natural extensions of these functions.
Keisler then gives a few examples of real statements to which the principle applies:
- Closure law for addition: for any x and y, the sum x + y is defined.
- Commutative law for addition: x + y = y + x.
- A rule for order: if 0 < x < y then 0 < 1/y < 1/x.
- Division by zero is never allowed: x/0 is undefined.
- An algebraic identity:
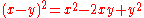 .
. - A trigonometric identity:
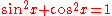 .
. - A rule for logarithms: If x > 0 and y > 0, then
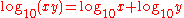 .
.
See also
- Criticism of non-standard analysisCriticism of non-standard analysisNon-standard analysis and its offshoot, non-standard calculus, have been criticized by several authors. The evaluation of non-standard analysis in the literature has varied greatly...
- Influence of non-standard analysisInfluence of non-standard analysisThe influence of Abraham Robinson's theory of non-standard analysis has been felt in a number of fields.-Probability theory:"Radically elementary probability theory" of Edward Nelson combines the discrete and the continuous theory through the infinitesimal approach...
- Non-standard calculusNon-standard calculusIn mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...
- Increment theoremIncrement theoremIn non-standard analysis, a field of mathematics, the increment theorem states the following: Suppose a function y = f is differentiable at x and that Δx is infinitesimal...

