Electron degeneracy pressure
Encyclopedia
Electron degeneracy pressure is a particular manifestation of the more general phenomenon of quantum degeneracy pressure. The Pauli Exclusion Principle
disallows two half integer spin particles (fermions) from occupying the same quantum state at a given time. The resulting emergent repulsive force is manifested as a pressure against compression of matter into smaller volumes of space. Electron degeneracy pressure results from the same underlying mechanism which defines the electron orbital structure of elemental matter. Freeman Dyson
showed that the imperviousness of solid matter is due to quantum degeneracy pressure rather than electrostatic repulsion as had been previously assumed. Furthermore electron degeneracy pressure prevents stars collapsing under their own weight once nuclear fusion has ceased. For stars which are sufficiently large electron degeneracy pressure is not sufficient to prevent the collapse of a star and a neutron star
is formed. In this case neutron degeneracy pressure prevents the star collapsing further.
When electrons are squeezed too close together, the exclusion principle requires them to have different energy levels. To add another electron to a given volume requires raising an electron's energy level to make room, and this requirement for energy to compress the material appears as a pressure.
Electron degeneracy pressure in a material can be computed as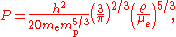
where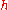
is Planck's constant, 
is the mass of the electron
,
is the mass of the proton
,
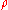is the density, and 
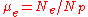is the ratio of electron number to proton number. (When particle energies reach relativistic
levels, a modified formula is required.)
This degeneracy pressure is omnipresent and is in addition to the normal gas pressure
. At commonly encountered densities, this pressure is so low that it can be neglected. Matter is electron degenerate when the density (proportional to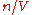 
) is high enough, and the temperature low enough, that the sum is dominated by the degeneracy pressure.
Also relevant to the understanding of electron degeneracy pressure is the Heisenberg uncertainty principle, which states that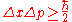
where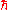
is Planck's constant (h) divided by 2π
, Δx is the uncertainty of the position measurements and Δp is the uncertainty (standard deviation
) of the momentum
measurements.
A material subjected to ever increasing pressure will become ever more compressed, and for electrons within it, the uncertainty in position measurements, Δx, becomes ever smaller. Thus, as dictated by the uncertainty principle, the uncertainty in the momenta of the electrons, Δp, becomes larger. Thus, no matter how low the temperature drops, the electrons must be traveling at this "Heisenberg speed", contributing to the pressure. When the pressure due to the "Heisenberg speed" exceeds that of the pressure from the thermal motions of the electrons, the electrons are referred to as degenerate, and the material is termed degenerate matter
.
Electron degeneracy pressure will halt the gravitational collapse of a star
if its mass
is below the Chandrasekhar Limit
(1.38 solar masses). This is the pressure that prevents a white dwarf
star from collapsing. A star exceeding this limit and without usable nuclear fuel will continue to collapse to form either a neutron star
or black hole
, because the degeneracy pressure provided by the electrons is weaker than the inward pull of gravity.
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
disallows two half integer spin particles (fermions) from occupying the same quantum state at a given time. The resulting emergent repulsive force is manifested as a pressure against compression of matter into smaller volumes of space. Electron degeneracy pressure results from the same underlying mechanism which defines the electron orbital structure of elemental matter. Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
showed that the imperviousness of solid matter is due to quantum degeneracy pressure rather than electrostatic repulsion as had been previously assumed. Furthermore electron degeneracy pressure prevents stars collapsing under their own weight once nuclear fusion has ceased. For stars which are sufficiently large electron degeneracy pressure is not sufficient to prevent the collapse of a star and a neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
is formed. In this case neutron degeneracy pressure prevents the star collapsing further.
When electrons are squeezed too close together, the exclusion principle requires them to have different energy levels. To add another electron to a given volume requires raising an electron's energy level to make room, and this requirement for energy to compress the material appears as a pressure.
Electron degeneracy pressure in a material can be computed as
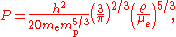
where
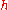is Planck's constant, is the mass of the electronElectron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
,
is the mass of the protonProton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
,
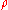is the density, and 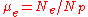is the ratio of electron number to proton number. (When particle energies reach relativisticTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
levels, a modified formula is required.)
This degeneracy pressure is omnipresent and is in addition to the normal gas pressure
. At commonly encountered densities, this pressure is so low that it can be neglected. Matter is electron degenerate when the density (proportional to 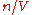) is high enough, and the temperature low enough, that the sum is dominated by the degeneracy pressure.Also relevant to the understanding of electron degeneracy pressure is the Heisenberg uncertainty principle, which states that
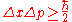
where
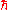is Planck's constant (h) divided by 2πPi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, Δx is the uncertainty of the position measurements and Δp is the uncertainty (standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
) of the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
measurements.
A material subjected to ever increasing pressure will become ever more compressed, and for electrons within it, the uncertainty in position measurements, Δx, becomes ever smaller. Thus, as dictated by the uncertainty principle, the uncertainty in the momenta of the electrons, Δp, becomes larger. Thus, no matter how low the temperature drops, the electrons must be traveling at this "Heisenberg speed", contributing to the pressure. When the pressure due to the "Heisenberg speed" exceeds that of the pressure from the thermal motions of the electrons, the electrons are referred to as degenerate, and the material is termed degenerate matter
Degenerate matter
Degenerate matter is matter that has such extraordinarily high density that the dominant contribution to its pressure is attributable to the Pauli exclusion principle. The pressure maintained by a body of degenerate matter is called the degeneracy pressure, and arises because the Pauli principle...
.
Electron degeneracy pressure will halt the gravitational collapse of a star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
if its mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
is below the Chandrasekhar Limit
Chandrasekhar limit
When a star starts running out of fuel, it usually cools off and collapses into one of three compact forms, depending on its total mass:* a White Dwarf, a big lump of Carbon and Oxygen atoms, almost like one huge molecule...
(1.38 solar masses). This is the pressure that prevents a white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
star from collapsing. A star exceeding this limit and without usable nuclear fuel will continue to collapse to form either a neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
or black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
, because the degeneracy pressure provided by the electrons is weaker than the inward pull of gravity.