
Eisenstein integral
Encyclopedia
In mathematical representation theory, the Eisenstein integral is an integral introduced by in the representation theory of semisimple Lie groups, analogous to Eisenstein series
in the theory of automorphic forms.
used Eisenstein integrals to decompose the regular representation of a semisimple Lie group into representations induced from parabolic subgroups.
gave a survey of Harish-Chandra's work on this.
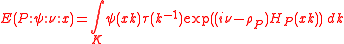
where:
Eisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
in the theory of automorphic forms.
used Eisenstein integrals to decompose the regular representation of a semisimple Lie group into representations induced from parabolic subgroups.
gave a survey of Harish-Chandra's work on this.
Definition
defined the Eisenstein integral by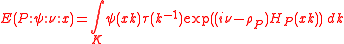
where:
- x is an element of a semisimple group G
- P = MAN is a cuspidal parabolic subgroup of G
- ν is an element of the complexification of a
- a is the Lie algebra of A in the Langlands decomposition P = MAN.
- K is a maximal compact subgroup of G, with G = KP.
- ψ is a cuspidal function on M, satisfying some extra conditions
- τ is a finite dimensional unitary double representation of K
- HP(x) = log a where x = kman is the decomposition of x in G = KMAN.

