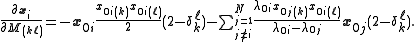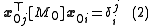Eigenvalue perturbation
Encyclopedia
In mathematics, eigenvalue perturbation is a perturbation
approach to finding eigenvalues and eigenvectors of systems perturbed from one with known eigenvectors and eigenvalues. It also allows one to determine the sensitivity of the eigenvalues and eigenvectors with respect to changes in the system. The following derivations are essentially self-contained and can be found in many texts on numerical linear algebra or numerical functional analysis.
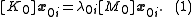
That is, we know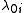 and
and 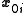 for
for 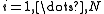 . Now suppose we want to change the matrices by a small amount. That is, we want to let
. Now suppose we want to change the matrices by a small amount. That is, we want to let
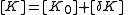
and
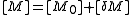
where all of the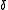 terms are much smaller than the corresponding term. We expect answers to be of the form
terms are much smaller than the corresponding term. We expect answers to be of the form
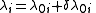
and
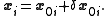
where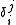 is the Kronecker delta.
is the Kronecker delta.
Now we want to solve the equation
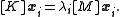
Substituting, we get
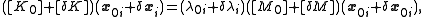
which expands to
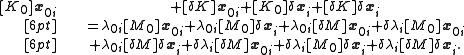
Canceling from (1) leaves
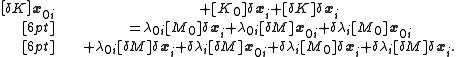
Removing the higher-order terms, this simplifies to
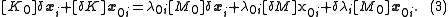
When the matrix is symmetric, the unperturbed eigenvectors are orthogonal and so we use them as a basis for the perturbed eigenvectors. That is, we want to construct
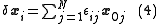
where the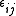 are small constants that are to be determined. Substituting (4) into (3) and rearranging gives
are small constants that are to be determined. Substituting (4) into (3) and rearranging gives
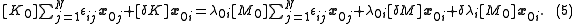
Or: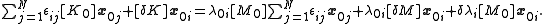
By equation (1):
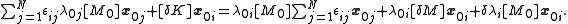
Because the eigenvectors are orthogonal, we can remove the summations by left multiplying by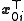 :
:
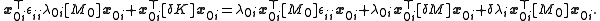
By use of equation (1) again:
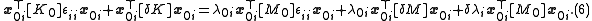
The two terms containing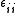 are equal because left-multiplying (1) by
are equal because left-multiplying (1) by 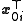 gives
gives
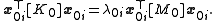
Canceling those terms in (6) leaves
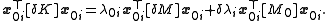
Rearranging gives
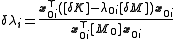
But by (2), this denominator is equal to 1. Thus
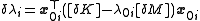 ■
■
Then, by left multiplying equation (6) by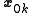 (for
(for 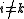 ):
):
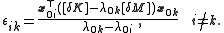
Or by changing the name of the indices:
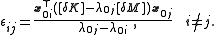
To find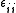 , use
, use
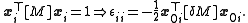
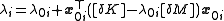
and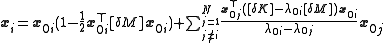
for infinetesimal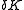 and
and 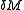 (the high order terms in (3) being negligible)
(the high order terms in (3) being negligible)
on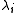 as a function of changes in the entries of the matrices. (Recall that the matrices are symmetric and so changing
as a function of changes in the entries of the matrices. (Recall that the matrices are symmetric and so changing 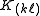 will also change
will also change 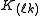 , hence the
, hence the  term.)
term.)
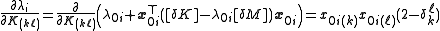
and

Similarly
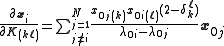
and
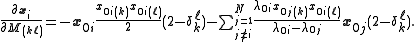
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
approach to finding eigenvalues and eigenvectors of systems perturbed from one with known eigenvectors and eigenvalues. It also allows one to determine the sensitivity of the eigenvalues and eigenvectors with respect to changes in the system. The following derivations are essentially self-contained and can be found in many texts on numerical linear algebra or numerical functional analysis.
Example
Suppose we have solutions to the generalized eigenvalue problem,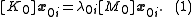
That is, we know
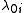 and
and 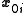 for
for 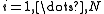 . Now suppose we want to change the matrices by a small amount. That is, we want to let
. Now suppose we want to change the matrices by a small amount. That is, we want to let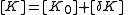
and
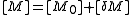
where all of the
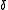 terms are much smaller than the corresponding term. We expect answers to be of the form
terms are much smaller than the corresponding term. We expect answers to be of the form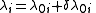
and
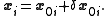
Steps
We assume that the matrices are symmetric and positive definite and assume we have scaled the eigenvectors such thatwhere
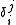 is the Kronecker delta.
is the Kronecker delta.Now we want to solve the equation
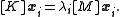
Substituting, we get
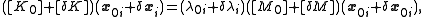
which expands to
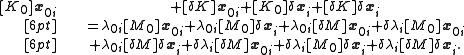
Canceling from (1) leaves
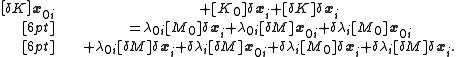
Removing the higher-order terms, this simplifies to
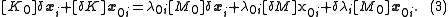
When the matrix is symmetric, the unperturbed eigenvectors are orthogonal and so we use them as a basis for the perturbed eigenvectors. That is, we want to construct
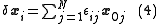
where the
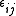 are small constants that are to be determined. Substituting (4) into (3) and rearranging gives
are small constants that are to be determined. Substituting (4) into (3) and rearranging gives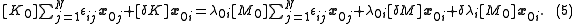
Or:
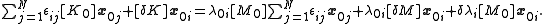
By equation (1):
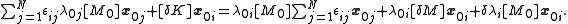
Because the eigenvectors are orthogonal, we can remove the summations by left multiplying by
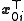 :
: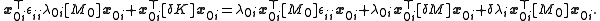
By use of equation (1) again:
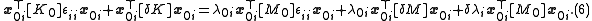
The two terms containing
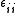 are equal because left-multiplying (1) by
are equal because left-multiplying (1) by 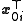 gives
gives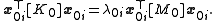
Canceling those terms in (6) leaves
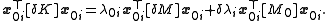
Rearranging gives
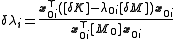
But by (2), this denominator is equal to 1. Thus
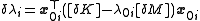 ■
■Then, by left multiplying equation (6) by
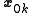 (for
(for 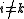 ):
):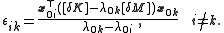
Or by changing the name of the indices:
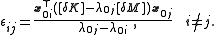
To find
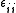 , use
, use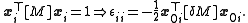
Summary
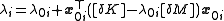
and
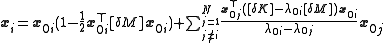
for infinetesimal
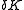 and
and 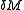 (the high order terms in (3) being negligible)
(the high order terms in (3) being negligible)Results
This means it is possible to efficiently do a sensitivity analysisSensitivity analysis
Sensitivity analysis is the study of how the variation in the output of a statistical model can be attributed to different variations in the inputs of the model. Put another way, it is a technique for systematically changing variables in a model to determine the effects of such changes.In any...
on
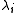 as a function of changes in the entries of the matrices. (Recall that the matrices are symmetric and so changing
as a function of changes in the entries of the matrices. (Recall that the matrices are symmetric and so changing 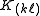 will also change
will also change 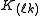 , hence the
, hence the  term.)
term.)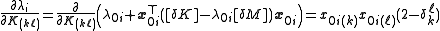
and

Similarly
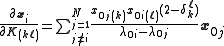
and