EHP spectral sequence
Encyclopedia
In mathematics, the EHP spectral sequence is a spectral sequence
used for inductively calculating the homotopy groups of spheres
localized at some prime
p. It is described in more detail in and . It is related to the EHP long exact sequence of ; the name "EHP" comes from the fact that Whitehead named 3 of the maps of his sequence "E" (the first letter of the German word "Einhängung" meaning "suspension"), "H" (for Hopf, as this map is the second Hopf-James invariant), and "P" (related to (Whitehead) products).
For p = 2 the spectral sequence uses some exact sequences associated to the fibration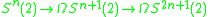
(where Ω stands for a loop space and the (2) is localization of a topological space
at the prime 2).
This gives a spectral sequence with E1k,n term πk+n(S2n−1(2)) and converging to π*S(2) (stable homotopy of spheres localized at 2). The spectral sequence has the advantage that the input is previously calculated homotopy groups. It was used by to calculate the first 31 stable homotopy groups of spheres.
For arbitrary primes one uses some fibrations found by :
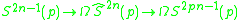
where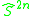
is the 2np − 1 skeleton of the loop space 
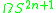. (For p = 2, 
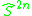is the same as 
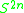, so Toda's fibrations at p = 2 are same same as the James fibrations.)
Spectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
used for inductively calculating the homotopy groups of spheres
Homotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
localized at some prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p. It is described in more detail in and . It is related to the EHP long exact sequence of ; the name "EHP" comes from the fact that Whitehead named 3 of the maps of his sequence "E" (the first letter of the German word "Einhängung" meaning "suspension"), "H" (for Hopf, as this map is the second Hopf-James invariant), and "P" (related to (Whitehead) products).
For p = 2 the spectral sequence uses some exact sequences associated to the fibration
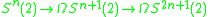
(where Ω stands for a loop space and the (2) is localization of a topological space
Localization of a topological space
In mathematics, well behaved topological spaces can be localized at primes, in a similar way to the localization of a ring at a prime. This construction was described by Dennis Sullivan in 1970 lecture notes that were finally published in ....
at the prime 2).
This gives a spectral sequence with E1k,n term πk+n(S2n−1(2)) and converging to π*S(2) (stable homotopy of spheres localized at 2). The spectral sequence has the advantage that the input is previously calculated homotopy groups. It was used by to calculate the first 31 stable homotopy groups of spheres.
For arbitrary primes one uses some fibrations found by :
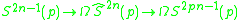
where
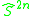is the 2np − 1 skeleton of the loop space 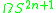. (For p = 2, 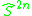is the same as 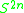, so Toda's fibrations at p = 2 are same same as the James fibrations.)