
Dynamic perfect hashing
Encyclopedia
In computer science
, dynamic perfect hashing is a programming technique for resolving collisions in a hash table
data structure
. This technique is useful for situations where fast queries, insertions, and deletions must be made on a large set, S, of elements.
is selected at random from a universal hash function set so that it is collision-free (i.e. a perfect hash function
). Therefore, the look-up cost is guaranteed to be O(1)
in the worst-case.
function Locate(x) is
j = h(x);
if (position hj(x) of subtable Tj contains x (not deleted))
return (x is in S);
end if
else
return (x is not in S);
end else
end
Although each second-level table requires quadratic space, if the keys inserted into the first-level hash table are uniformly distributed, the structure as a whole occupies expected O(n) space, since bucket sizes are small with high probability
.
During the insertion of a new entry x at j, the global operations counter, count, is incremented. If x exists at j but is marked as deleted then the mark is removed. If x exists at j, or at the subtable Tj, but is not marked as deleted then a collision is said to occur and the jth bucket's second-level table Tj is rebuilt with a different randomly-selected hash function hj. Because the load factor of the second-level table is kept low (1/k), rebuilding is infrequent, and the amortized
cost of insertions is O(1).
function Insert(x) is
count = count + 1;
if (count > M)
FullRehash(x);
end if
else
j = h(x);
if (Position hj(x) of subtable Tj contains x)
if (x is marked deleted)
remove the delete marker;
end if
end if
else
bj = bj + 1;
if (bj <= mj)
if position hj(x) of Tj is empty
store x in position hj(x) of Tj;
end if
else
Put all unmarked elements of Tj in list Lj;
Append x to list Lj;
bj = length of Lj;
repeat
hj = randomly chosen function in Hsj;
until hj is injective on the elements of Lj;
for all y on list Lj
store y in position hj(y) of Tj;
end for
end else
end if
else
mj = 2 * max{1, mj};
sj = 2 * mj * (mj - 1);
if the sum total of all sj ≤ 32 * M2 / s(M) + 4 * M
Allocate sj cells for Tj;
Put all unmarked elements of Tj in list Lj;
Append x to list Lj;
bj = length of Lj;
repeat
hj = randomly chosen function in Hsj;
until hj is injective on the elements of Lj;
for all y on list Lj
store y in position hj(y) of Tj;
end for
end if
else
FullRehash(x);
end else
end else
end else
end else
end
Deletion of x simply flags x as deleted without removal and increments count. In the case of both insertions and deletions, if count reaches a threshold M the entire table is rebuilt, where M is some constant multiple of the size of S at the start of a new phase. Here phase refers to the time between full rebuilds. The amortized cost of delete is O(1). Note that here the -1 in "Delete(x)" is a representation of an element which is not in the set of all possible elements U.
function Delete(x) is
count = count + 1;
j = h(x);
if position h(x) of subtable Tj contains x
mark x as deleted;
end if
else
return (x is not a member of S);
end else
if (count >= M)
FullRehash(-1);
end if
end
A full rebuild of the table of S first starts by removing all elements marked as deleted and then setting the next threshold value M to some constant multiple of the size of S. A hash function, which partitions S into s(M) subsets, where the size of subset j is sj, is repeatedly randomly chosen until:
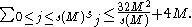
Finally, for each subtable Tj a hash function hj is repeatedly randomly chosen from Hsj until hj is injective on the elements of Tj. The expected time for a full rebuild of the table of S with size n is O(n).
function FullRehash(x) is
Put all unmarked elements of T in list L;
if (x is in U)
append x to L;
end if
count = length of list L;
M = (1 + c) * max{count, 4};
repeat
h = randomly chosen function in Hs(M);
for all j < s(M)
form a list Lj for h(x) = j;
bj = length of Lj;
mj = 2 * bj;
sj = 2 * mj * (mj - 1);
end for
until the sum total of all sj ≤ 32 * M2 / s(M) + 4 * M
for all j < s(M)
Allocate space sj for subtable Tj;
repeat
hj = randomly chosen function in Hsj;
until hj is injective on the elements of list Lj;
end for
for all x on list Lj
store x in position hj(x) of Tj;
end for
end
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, dynamic perfect hashing is a programming technique for resolving collisions in a hash table
Hash table
In computer science, a hash table or hash map is a data structure that uses a hash function to map identifying values, known as keys , to their associated values . Thus, a hash table implements an associative array...
data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
. This technique is useful for situations where fast queries, insertions, and deletions must be made on a large set, S, of elements.
Details
In this method, the entries that hash to the same slot of the table are organized as separate second-level hash table. If there are k entries in this set S, the second-level table is allocated with k2 slots, and its hash functionHash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
is selected at random from a universal hash function set so that it is collision-free (i.e. a perfect hash function
Perfect hash function
A perfect hash function for a set S is a hash function that maps distinct elements in S to a set of integers, with no collisions. A perfect hash function has many of the same applications as other hash functions, but with the advantage that no collision resolution has to be implemented.- Properties...
). Therefore, the look-up cost is guaranteed to be O(1)
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
in the worst-case.
function Locate(x) is
j = h(x);
if (position hj(x) of subtable Tj contains x (not deleted))
return (x is in S);
end if
else
return (x is not in S);
end else
end
Although each second-level table requires quadratic space, if the keys inserted into the first-level hash table are uniformly distributed, the structure as a whole occupies expected O(n) space, since bucket sizes are small with high probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
.
During the insertion of a new entry x at j, the global operations counter, count, is incremented. If x exists at j but is marked as deleted then the mark is removed. If x exists at j, or at the subtable Tj, but is not marked as deleted then a collision is said to occur and the jth bucket's second-level table Tj is rebuilt with a different randomly-selected hash function hj. Because the load factor of the second-level table is kept low (1/k), rebuilding is infrequent, and the amortized
Amortized analysis
In computer science, amortized analysis is a method of analyzing algorithms that considers the entire sequence of operations of the program. It allows for the establishment of a worst-case bound for the performance of an algorithm irrespective of the inputs by looking at all of the operations...
cost of insertions is O(1).
function Insert(x) is
count = count + 1;
if (count > M)
FullRehash(x);
end if
else
j = h(x);
if (Position hj(x) of subtable Tj contains x)
if (x is marked deleted)
remove the delete marker;
end if
end if
else
bj = bj + 1;
if (bj <= mj)
if position hj(x) of Tj is empty
store x in position hj(x) of Tj;
end if
else
Put all unmarked elements of Tj in list Lj;
Append x to list Lj;
bj = length of Lj;
repeat
hj = randomly chosen function in Hsj;
until hj is injective on the elements of Lj;
for all y on list Lj
store y in position hj(y) of Tj;
end for
end else
end if
else
mj = 2 * max{1, mj};
sj = 2 * mj * (mj - 1);
if the sum total of all sj ≤ 32 * M2 / s(M) + 4 * M
Allocate sj cells for Tj;
Put all unmarked elements of Tj in list Lj;
Append x to list Lj;
bj = length of Lj;
repeat
hj = randomly chosen function in Hsj;
until hj is injective on the elements of Lj;
for all y on list Lj
store y in position hj(y) of Tj;
end for
end if
else
FullRehash(x);
end else
end else
end else
end else
end
Deletion of x simply flags x as deleted without removal and increments count. In the case of both insertions and deletions, if count reaches a threshold M the entire table is rebuilt, where M is some constant multiple of the size of S at the start of a new phase. Here phase refers to the time between full rebuilds. The amortized cost of delete is O(1). Note that here the -1 in "Delete(x)" is a representation of an element which is not in the set of all possible elements U.
function Delete(x) is
count = count + 1;
j = h(x);
if position h(x) of subtable Tj contains x
mark x as deleted;
end if
else
return (x is not a member of S);
end else
if (count >= M)
FullRehash(-1);
end if
end
A full rebuild of the table of S first starts by removing all elements marked as deleted and then setting the next threshold value M to some constant multiple of the size of S. A hash function, which partitions S into s(M) subsets, where the size of subset j is sj, is repeatedly randomly chosen until:
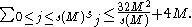
Finally, for each subtable Tj a hash function hj is repeatedly randomly chosen from Hsj until hj is injective on the elements of Tj. The expected time for a full rebuild of the table of S with size n is O(n).
function FullRehash(x) is
Put all unmarked elements of T in list L;
if (x is in U)
append x to L;
end if
count = length of list L;
M = (1 + c) * max{count, 4};
repeat
h = randomly chosen function in Hs(M);
for all j < s(M)
form a list Lj for h(x) = j;
bj = length of Lj;
mj = 2 * bj;
sj = 2 * mj * (mj - 1);
end for
until the sum total of all sj ≤ 32 * M2 / s(M) + 4 * M
for all j < s(M)
Allocate space sj for subtable Tj;
repeat
hj = randomly chosen function in Hsj;
until hj is injective on the elements of list Lj;
end for
for all x on list Lj
store x in position hj(x) of Tj;
end for
end

