Dvoretzky's theorem
Encyclopedia
In mathematics
, in the theory of Banach space
s, Dvoretzky's theorem is an important structural theorem proved by Aryeh Dvoretzky
in the early 1960s. It answered a question of Alexander Grothendieck
. A new proof found by Vitali Milman
in the 1970s was one of the starting points for the development of asymptotic geometric analysis (also called asymptotic functional analysis or the local theory of Banach spaces).
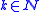and every 
there exists 
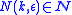such that if 
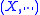is a Banach space of dimension
, there exist a subspace
of dimension 
and a positive quadratic form
on 
such that the corresponding
Euclidean norm
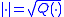
on
satisfies:
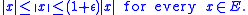
gave a new proof of Dvoretzky's theorem, making use of the concentration of measure
on the sphere to show that a random
-dimensional subspace satisfies the above inequality with probability very close to 
. The proof gives the sharp dependence on 
:
Equivalently, for every Banach space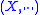
of dimension N, there exists a subspace 
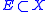of dimension
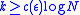and a Euclidean norm
on 
such that the inequality above holds.
More precisely, let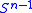
be the unit sphere with respect to some Euclidean structure 
, and let 
be the invariant probability measure on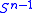 
. Then:
Here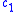
is a universal constant. The best possible 
is denoted 
and called the Dvoretzky dimension of 
.
The dependence on
was studied by Yehoram Gordon, who showed that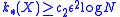 
. Another proof of this result was given by Gideon Schechtman.
Noga Alon
and Vitali Milman
showed that the logarithmic bound on the dimension of the subspace in Dvoretzky's theorem can be significantly improved, if one is willing to accept a subspace that is close either to a Euclidean space or to a Chebyshev space
. Specifically, for some constant c, every n-dimensional space has a subspace of dimension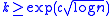
that is close eithe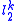r to 
or to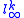 
.
Important related results were proved by Tadeusz Figiel, Joram Lindenstrauss
and Milman.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the theory of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, Dvoretzky's theorem is an important structural theorem proved by Aryeh Dvoretzky
Aryeh Dvoretzky
Aryeh Dvoretzky was a Russian-born Israeli mathematician, the winner of the 1973 Israel Prize in Mathematics. He is best known for his work in functional analysis, statistics and probability.-Biography:...
in the early 1960s. It answered a question of Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
. A new proof found by Vitali Milman
Vitali Milman
Vitali Davidovich Milman is a mathematician specializing in analysis. He is currently a professor at the Tel-Aviv University. In the past he was a President of the Israel Mathematical Union and a member of the “Aliyah” committee of Tel-Aviv University.-Work:Milman received in Ph.D...
in the 1970s was one of the starting points for the development of asymptotic geometric analysis (also called asymptotic functional analysis or the local theory of Banach spaces).
Original formulation
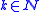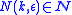For every and every there exists such that if 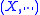is a Banach space of dimension, there exist a subspace of dimension and a positive quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on such that the correspondingEuclidean norm
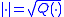
on
satisfies: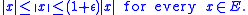Further development
In 1971, Vitali MilmanVitali Milman
Vitali Davidovich Milman is a mathematician specializing in analysis. He is currently a professor at the Tel-Aviv University. In the past he was a President of the Israel Mathematical Union and a member of the “Aliyah” committee of Tel-Aviv University.-Work:Milman received in Ph.D...
gave a new proof of Dvoretzky's theorem, making use of the concentration of measure
Concentration of measure
In mathematics, concentration of measure is a principle that is applied in measure theory, probability and combinatorics, and has consequences for other fields such as Banach space theory. Informally, it states that "A random variable that depends in a Lipschitz way on many independent variables ...
on the sphere to show that a random
-dimensional subspace satisfies the above inequality with probability very close to . The proof gives the sharp dependence on :Equivalently, for every Banach space
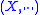of dimension N, there exists a subspace 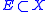of dimension 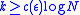and a Euclidean norm on such that the inequality above holds.More precisely, let
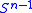be the unit sphere with respect to some Euclidean structure , and let be the invariant probability measure on 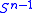. Then:
- There exists such a subspace
with
-
-
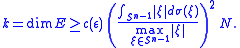
- For any
one may choose 
so that the term in the brackets will be at most
- For any
-
-
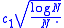
Here
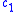is a universal constant. The best possible is denoted and called the Dvoretzky dimension of .The dependence on
was studied by Yehoram Gordon, who showed that 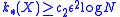. Another proof of this result was given by Gideon Schechtman.Noga Alon
Noga Alon
Noga Alon is an Israeli mathematician noted for his contributions to combinatorics and theoretical computer science, having authored hundreds of papers.- Academic background :...
and Vitali Milman
Vitali Milman
Vitali Davidovich Milman is a mathematician specializing in analysis. He is currently a professor at the Tel-Aviv University. In the past he was a President of the Israel Mathematical Union and a member of the “Aliyah” committee of Tel-Aviv University.-Work:Milman received in Ph.D...
showed that the logarithmic bound on the dimension of the subspace in Dvoretzky's theorem can be significantly improved, if one is willing to accept a subspace that is close either to a Euclidean space or to a Chebyshev space
Chebyshev distance
In mathematics, Chebyshev distance , Maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension...
. Specifically, for some constant c, every n-dimensional space has a subspace of dimension
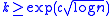that is close eithe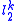r to or to 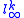.Important related results were proved by Tadeusz Figiel, Joram Lindenstrauss
Joram Lindenstrauss
Joram Lindenstrauss is an Israeli mathematician working in functional analysis. He is professor emeritus of mathematics at the Einstein Institute of Mathematics, Hebrew University of Jerusalem, Israel.-Biography:...
and Milman.