
Dividend Discount Model
Encyclopedia
The dividend discount model is a way of valuing a company based on the theory that a stock
is worth the discounted sum of all of its future dividend payments. In other words, it is used to evaluate stocks based on the net present value
of the future dividends.
Dividend discount model is a tool that produces a number based on the data provided. The equation can be written as
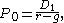
where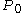 is the current stock price,
is the current stock price, 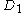 is the expected dividend,
is the expected dividend,  is the required rate of return, and
is the required rate of return, and 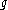 is the expected growth rate in perpetuity.
is the expected growth rate in perpetuity.
This equation is also used to estimate cost of capital
by solving for
From the first equation, one might notice that in the long run, the growth rate cannot exceed the cost of equity
; cannot be negative, i.e.,
cannot be negative, i.e.,  . In the short run if
. In the short run if  , then usually a two stage DDM is used:
, then usually a two stage DDM is used:
Therefore,
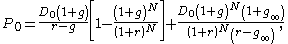
where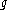 denotes the short-run expected growth rate,
denotes the short-run expected growth rate, 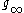 denotes the long-run growth rate, and
denotes the long-run growth rate, and 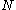 is the period (number of years), over which the short-run growth rate is applied.
is the period (number of years), over which the short-run growth rate is applied.
Stock
The capital stock of a business entity represents the original capital paid into or invested in the business by its founders. It serves as a security for the creditors of a business since it cannot be withdrawn to the detriment of the creditors...
is worth the discounted sum of all of its future dividend payments. In other words, it is used to evaluate stocks based on the net present value
Net present value
In finance, the net present value or net present worth of a time series of cash flows, both incoming and outgoing, is defined as the sum of the present values of the individual cash flows of the same entity...
of the future dividends.
Dividend discount model is a tool that produces a number based on the data provided. The equation can be written as
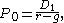
where
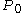 is the current stock price,
is the current stock price, 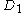 is the expected dividend,
is the expected dividend,  is the required rate of return, and
is the required rate of return, and 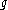 is the expected growth rate in perpetuity.
is the expected growth rate in perpetuity.This equation is also used to estimate cost of capital
Cost of capital
The cost of capital is a term used in the field of financial investment to refer to the cost of a company's funds , or, from an investor's point of view "the shareholder's required return on a portfolio of all the company's existing securities"...
by solving for

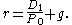
From the first equation, one might notice that in the long run, the growth rate cannot exceed the cost of equity
Cost of equity
In finance, the cost of equity is the return a firm theoretically pays to its equity investors, i.e., shareholders, to compensate for the risk they undertake by investing their capital. Firms need to acquire capital from others to operate and grow...
;
 cannot be negative, i.e.,
cannot be negative, i.e., 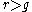 . In the short run if
. In the short run if 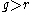 , then usually a two stage DDM is used:
, then usually a two stage DDM is used: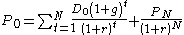
Therefore,
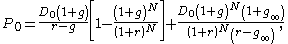
where
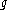 denotes the short-run expected growth rate,
denotes the short-run expected growth rate, 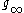 denotes the long-run growth rate, and
denotes the long-run growth rate, and 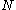 is the period (number of years), over which the short-run growth rate is applied.
is the period (number of years), over which the short-run growth rate is applied.

