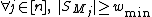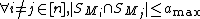Disjunct matrix
Encyclopedia
Disjunct and separable matrices play a pivotal role in the mathematical area of non-adaptive group testing
. This area investigates efficient designs and procedures to identify 'needles in haystacks' by conducting the tests on groups of items instead of each item alone. The main concept is that if there are very few special items (needles) and the groups are constructed according to certain combinatorial guidelines, then one can test the groups and find all the needles. This can reduce the cost and the labor associated with of large scale experiments.
The grouping pattern can be represented by a binary matrix, where each column represents an item and each row represents a pool. The symbol '1' denotes participation in the pool and '0' absence from a pool. The d-disjuntness and the d-separability of the matrix describe sufficient condition to identify d special items.
binary matrix, where each column represents an item and each row represents a pool. The symbol '1' denotes participation in the pool and '0' absence from a pool. The d-disjuntness and the d-separability of the matrix describe sufficient condition to identify d special items.
In a matrix that is d-separable, the Boolean sum of every d columns is unique. In a matrix that is d-disjunct the Boolean sum of every d columns does not contain any other column in the matrix. Theoretically, for the same number of columns (items), one can construct d-separable matrices with fewer rows (tests) than d-disjunct. However, designs that are based on d-separable are less applicable since the decoding time to identify the special items is exponential. In contrast, the decoding time for d-dijunct matrices is polynomial.
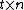 matrix
matrix  is
is 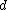 -separable if and only if
-separable if and only if 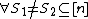 where
where  such that
such that 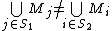
Group testing: Given input and
and  such that
such that 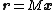 output
output 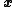
This formalizes the relation between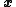 and the columns of
and the columns of 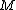 and
and  in a way more suitable to the thinking of
in a way more suitable to the thinking of 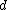 -separable and
-separable and  -disjunct matrices. The algorithm to decode a
-disjunct matrices. The algorithm to decode a 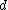 -separable matrix is as follows:
-separable matrix is as follows:
Given a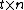 matrix
matrix 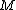 such that
such that 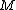 is
is 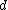 -separable:
-separable:
This algorithm runs in time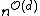 .
.
Definition: A x
x  matrix
matrix 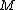 is d-disjunct if
is d-disjunct if 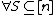 such that
such that 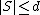 ,
, 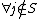
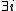 such that
such that 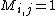 but
but 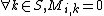 .
.
Denoting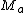 is the
is the  column of
column of 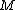 and
and 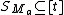 where
where 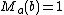 if and only if
if and only if  gives that
gives that 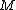 is
is 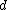 -disjunct if and only if
-disjunct if and only if 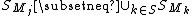
Claim: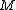 is
is 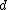 -disjunct implies
-disjunct implies 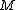 is
is 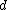 -separable
-separable
Proof: (by contradiction) Let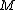 be a
be a  x
x 
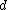 -disjunct matrix. Assume for contradiction that
-disjunct matrix. Assume for contradiction that 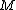 is not
is not 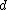 -separable. Then there exists
-separable. Then there exists 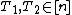 and
and 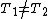 with
with 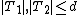 such that
such that 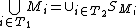 . This implies that
. This implies that 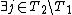 such that
such that 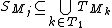 . This contradicts the fact that
. This contradicts the fact that 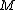 is
is 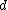 -disjunct. Therefore
-disjunct. Therefore 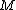 is
is 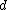 -separable.
-separable. 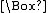
 -separable matrices was still a polynomial in
-separable matrices was still a polynomial in  . The following will give a nicer algorithm for
. The following will give a nicer algorithm for 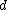 -disjunct matrices which will be a
-disjunct matrices which will be a 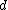 multiple instead of raised to the power of
multiple instead of raised to the power of 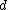 given our bounds for
given our bounds for  . The algorithm is as follows in the proof of the following lemma:
. The algorithm is as follows in the proof of the following lemma:
Lemma 1: There exists an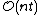 time decoding for any
time decoding for any  -disjunct
-disjunct  x
x  matrix.
matrix.
Proof of Lemma 1: Given as input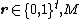 use the following algorithm:
use the following algorithm:
By Observation 1 we get that any position where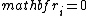 the appropriate
the appropriate 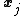 's will be set to 0 by step 2 of the algorithm. By Observation 2 we have that there is at least one
's will be set to 0 by step 2 of the algorithm. By Observation 2 we have that there is at least one  such that if
such that if 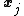 is supposed to be 1 then
is supposed to be 1 then 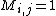 and, if
and, if 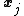 is supposed to be 1, it can only be the case that
is supposed to be 1, it can only be the case that 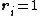 as well. Therefore step 2 will never assign
as well. Therefore step 2 will never assign 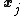 the value 0 leaving it as a 1 and solving for
the value 0 leaving it as a 1 and solving for  . This takes time
. This takes time 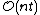 overall.
overall. 
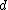 -disjunct matrices. Not only are the upper bounds nice, but from Lemma 1 we know that there is also a nice decoding algorithm for these bounds. First the following lemma will be proved since it is relied upon for both constructions:
-disjunct matrices. Not only are the upper bounds nice, but from Lemma 1 we know that there is also a nice decoding algorithm for these bounds. First the following lemma will be proved since it is relied upon for both constructions:
Lemma 2: Given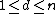 let
let 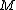 be a
be a 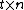 matrix and:
matrix and:
for some integers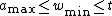 then
then 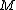 is
is 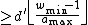 -disjunct.
-disjunct.
Note: these conditions are stronger than simply having a subset of size but rather applies to any pair of columns in a matrix. Therefore no matter what column
but rather applies to any pair of columns in a matrix. Therefore no matter what column 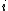 that is chosen in the matrix, that column will contain at least
that is chosen in the matrix, that column will contain at least  1's and the total number of shared 1's by any two columns is
1's and the total number of shared 1's by any two columns is  .
.
Proof of Lemma 2: Fix an arbitrary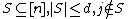 and a matrix
and a matrix 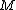 . There exists a match between
. There exists a match between 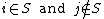 if column
if column 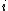 has a 1 in the same row position as in column
has a 1 in the same row position as in column 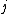 . Then the total number of matches is
. Then the total number of matches is  , i.e. a column
, i.e. a column 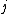 has a fewer number of matches than the number of ones in it. Therefore there must be a row with all 0s in
has a fewer number of matches than the number of ones in it. Therefore there must be a row with all 0s in 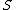 but a 1 in
but a 1 in 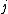 .
. 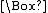
We will now generate constructions for the bounds.
. Using this randomized construction gives that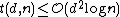 . The following lemma will give the result needed.
. The following lemma will give the result needed.
Theorem 1: There exists a random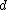 -disjunct matrix with
-disjunct matrix with  rows.
rows.
Proof of Theorem 1: Begin by building a random matrix
matrix 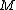 with
with 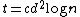 (where
(where  will be picked later). It will be shown that
will be picked later). It will be shown that 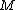 is
is 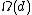 -disjunct. First note that
-disjunct. First note that 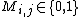 and let
and let  independently with probability
independently with probability 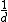 for
for 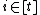 and
and 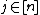 . Now fix
. Now fix 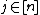 . Denote the
. Denote the 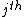 column of
column of  as
as  . Then the expectancy is
. Then the expectancy is 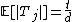 . Using the Chernoff bound, with
. Using the Chernoff bound, with 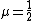 , gives
, gives 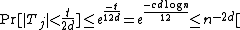 if
if 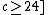 . Taking the union bound
. Taking the union bound
over all columns gives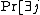 ,
, 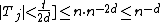 . This gives
. This gives  ,
,  . Therefore
. Therefore 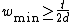 with probability
with probability  .
.
Now suppose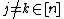 and
and 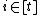 then
then 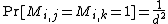 . So
. So 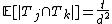 . Using the Chernoff bound on this gives
. Using the Chernoff bound on this gives  if
if  . By the union bound over
. By the union bound over 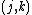 pairs
pairs 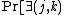 such that
such that  . This gives that
. This gives that 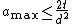 and
and 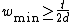 with probability
with probability 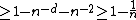 . Note that by changing
. Note that by changing  the probability
the probability 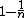 can be made to be
can be made to be 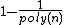 . Thus
. Thus 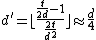 . By setting
. By setting 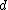 to be
to be  , the above argument shows that
, the above argument shows that 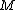 is
is 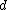 -disjunct.
-disjunct.
Note that in this proof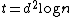 thus giving the upper bound of
thus giving the upper bound of 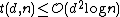 .
. 
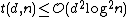 using a strongly explicit code. Although this bound is worse by a
using a strongly explicit code. Although this bound is worse by a 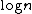 factor it is preferable because this produces a strongly explicit construction instead of a randomized one.
factor it is preferable because this produces a strongly explicit construction instead of a randomized one.
Theorem 2: There exists a strongly explicit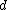 -disjunct matrix with
-disjunct matrix with 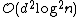 rows.
rows.
This proof will use the properties of concatenated codes along with the properties of disjunct matrices to construct a code that will satisfy the bound we are after.
Proof of Theorem 2:
Let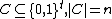 such that
such that 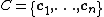 . Denote
. Denote 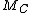 as the matrix with its
as the matrix with its 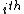 column being
column being 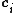 . If
. If 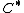 can be found such that
can be found such that
then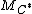 is
is  -disjunct. To complete the proof another concept must be introduced. This concept uses code concatenation to obtain the result we want.
-disjunct. To complete the proof another concept must be introduced. This concept uses code concatenation to obtain the result we want.
Kautz-Singleton '64
Let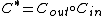 . Let
. Let 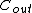 be a
be a  -Reed–Solomon code. Let
-Reed–Solomon code. Let  such that for
such that for 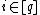 ,
, 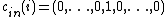 where the 1 is in the
where the 1 is in the 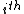 position. Then
position. Then  ,
, 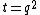 , and
, and 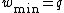 .
.
---
Example: Let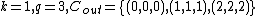 . Below,
. Below, 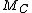 denotes the matrix of codewords for
denotes the matrix of codewords for 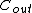 and
and 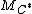 denotes the matrix of codewords for
denotes the matrix of codewords for 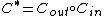 , where each column is a codeword. The overall image shows the transition from the outer code to the concatenated code.
, where each column is a codeword. The overall image shows the transition from the outer code to the concatenated code.
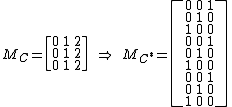
---
Divide the rows of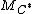 into sets of size
into sets of size 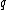 and number them as
and number them as 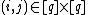 where
where 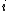 indexes the set of rows and
indexes the set of rows and 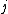 indexes the row in the set. If
indexes the row in the set. If 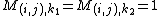 then note that
then note that 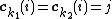 where
where 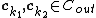 . So that means
. So that means 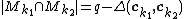 . Since
. Since 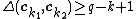 it gives that
it gives that 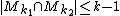 so let
so let 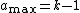 . Since
. Since  , the entries in each column of
, the entries in each column of 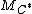 can be looked at as
can be looked at as 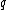 sets of
sets of  entries where only one of the entries is nonzero (by definition of
entries where only one of the entries is nonzero (by definition of 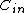 ) which gives a total of
) which gives a total of 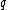 nonzero entries in each column. Therefore
nonzero entries in each column. Therefore 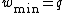 and
and 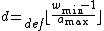 (so
(so 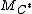 is
is  -disjunct).
-disjunct).
Now pick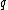 and
and 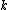 such that
such that  (so
(so 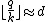 ). Since
). Since 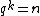 we have
we have 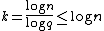 . Since
. Since 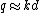 and
and 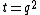 it gives that
it gives that 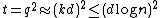 .
. 
Thus we have a strongly explicit construction for a code that can be used to form a group testing matrix and so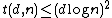 .
.
For non-adaptive testing we have shown that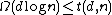 and we have that (i)
and we have that (i) 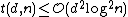 (strongly explicit) and (ii)
(strongly explicit) and (ii) 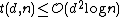 (randomized). As of recent work by Porat and Rothscheld they presented a explicit method construction (i.e. deterministic time but not strongly explicit) for
(randomized). As of recent work by Porat and Rothscheld they presented a explicit method construction (i.e. deterministic time but not strongly explicit) for 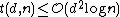 , however it is not shown here. There is also a lower bound for disjunct matrices of
, however it is not shown here. There is also a lower bound for disjunct matrices of 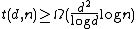 which is not shown here either.
which is not shown here either.
Group testing
In combinatorial mathematics, group testing is a set of problems with the objective of reducing the cost of identifying certain elements of a set.-Background:Robert Dorfman's paper in 1943 introduced the field of Group Testing...
. This area investigates efficient designs and procedures to identify 'needles in haystacks' by conducting the tests on groups of items instead of each item alone. The main concept is that if there are very few special items (needles) and the groups are constructed according to certain combinatorial guidelines, then one can test the groups and find all the needles. This can reduce the cost and the labor associated with of large scale experiments.
The grouping pattern can be represented by a
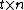 binary matrix, where each column represents an item and each row represents a pool. The symbol '1' denotes participation in the pool and '0' absence from a pool. The d-disjuntness and the d-separability of the matrix describe sufficient condition to identify d special items.
binary matrix, where each column represents an item and each row represents a pool. The symbol '1' denotes participation in the pool and '0' absence from a pool. The d-disjuntness and the d-separability of the matrix describe sufficient condition to identify d special items.In a matrix that is d-separable, the Boolean sum of every d columns is unique. In a matrix that is d-disjunct the Boolean sum of every d columns does not contain any other column in the matrix. Theoretically, for the same number of columns (items), one can construct d-separable matrices with fewer rows (tests) than d-disjunct. However, designs that are based on d-separable are less applicable since the decoding time to identify the special items is exponential. In contrast, the decoding time for d-dijunct matrices is polynomial.
d-separable
Definition: A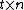 matrix
matrix  is
is 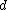 -separable if and only if
-separable if and only if 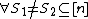 where
where  such that
such that 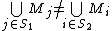
Decoding algorithm
First we will describe another way to look at the problem of group testing and how to decode it from a different notation. We can give a new interpretation of how group testing works as follows:Group testing: Given input
 and
and  such that
such that 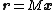 output
output 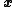
- Take
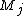 to be the
to be the 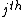 column of
column of 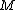
- Define
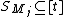 so that
so that  if and only if
if and only if 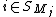
- This gives that
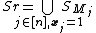
This formalizes the relation between
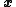 and the columns of
and the columns of 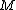 and
and  in a way more suitable to the thinking of
in a way more suitable to the thinking of 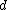 -separable and
-separable and  -disjunct matrices. The algorithm to decode a
-disjunct matrices. The algorithm to decode a 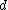 -separable matrix is as follows:
-separable matrix is as follows:Given a
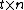 matrix
matrix 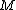 such that
such that 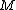 is
is 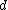 -separable:
-separable:
- For each
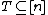 such that
such that 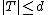 check if
check if 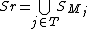
This algorithm runs in time
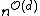 .
.d-disjunct
In literature disjunct matrices are also called super-imposed codes and d-cover-free families.Definition: A
 x
x  matrix
matrix 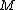 is d-disjunct if
is d-disjunct if 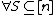 such that
such that 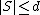 ,
, 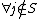
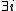 such that
such that 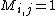 but
but 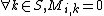 .
.Denoting
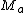 is the
is the  column of
column of 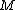 and
and 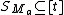 where
where 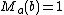 if and only if
if and only if  gives that
gives that 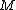 is
is 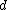 -disjunct if and only if
-disjunct if and only if 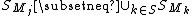
Claim:
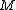 is
is 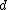 -disjunct implies
-disjunct implies 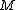 is
is 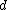 -separable
-separableProof: (by contradiction) Let
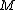 be a
be a  x
x 
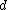 -disjunct matrix. Assume for contradiction that
-disjunct matrix. Assume for contradiction that 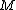 is not
is not 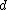 -separable. Then there exists
-separable. Then there exists 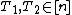 and
and 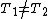 with
with 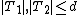 such that
such that 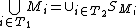 . This implies that
. This implies that 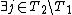 such that
such that 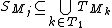 . This contradicts the fact that
. This contradicts the fact that 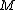 is
is 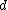 -disjunct. Therefore
-disjunct. Therefore 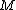 is
is 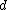 -separable.
-separable. 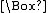
Decoding algorithm
The algorithm for -separable matrices was still a polynomial in
-separable matrices was still a polynomial in  . The following will give a nicer algorithm for
. The following will give a nicer algorithm for 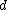 -disjunct matrices which will be a
-disjunct matrices which will be a 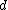 multiple instead of raised to the power of
multiple instead of raised to the power of 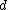 given our bounds for
given our bounds for  . The algorithm is as follows in the proof of the following lemma:
. The algorithm is as follows in the proof of the following lemma:Lemma 1: There exists an
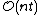 time decoding for any
time decoding for any  -disjunct
-disjunct  x
x  matrix.
matrix.
- Observation 1: For any matrix
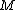 and given
and given  if
if 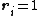 it implies
it implies 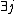 such that
such that 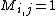 and
and 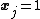 where
where 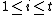 and
and 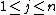 . The opposite is also true. If
. The opposite is also true. If 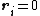 it implies
it implies 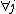 if
if 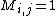 then
then 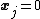 . This is the case because
. This is the case because  is generated by taking all of the logical or of the
is generated by taking all of the logical or of the 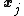 's where
's where 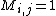 .
. - Observation 2: For any
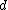 -disjunct matrix and every set
-disjunct matrix and every set 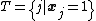 where
where 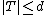 and for each
and for each  where
where 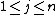 there exists some
there exists some  where
where 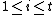 such that
such that 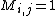 but
but 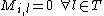 . Thus, if
. Thus, if 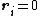 then
then 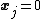 .
.
Proof of Lemma 1: Given as input
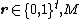 use the following algorithm:
use the following algorithm:
- For each
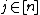 set
set 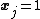
- For
 , if
, if  then for all
then for all 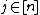 , if
, if 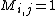 set
set 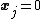
By Observation 1 we get that any position where
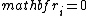 the appropriate
the appropriate 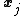 's will be set to 0 by step 2 of the algorithm. By Observation 2 we have that there is at least one
's will be set to 0 by step 2 of the algorithm. By Observation 2 we have that there is at least one  such that if
such that if 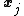 is supposed to be 1 then
is supposed to be 1 then 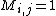 and, if
and, if 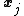 is supposed to be 1, it can only be the case that
is supposed to be 1, it can only be the case that 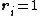 as well. Therefore step 2 will never assign
as well. Therefore step 2 will never assign 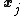 the value 0 leaving it as a 1 and solving for
the value 0 leaving it as a 1 and solving for  . This takes time
. This takes time 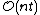 overall.
overall. 
Upper bounds for non-adaptive group testing
The results for these upper bounds rely mostly on the properties of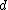 -disjunct matrices. Not only are the upper bounds nice, but from Lemma 1 we know that there is also a nice decoding algorithm for these bounds. First the following lemma will be proved since it is relied upon for both constructions:
-disjunct matrices. Not only are the upper bounds nice, but from Lemma 1 we know that there is also a nice decoding algorithm for these bounds. First the following lemma will be proved since it is relied upon for both constructions:Lemma 2: Given
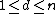 let
let 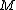 be a
be a 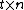 matrix and:
matrix and:
for some integers
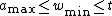 then
then 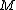 is
is 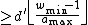 -disjunct.
-disjunct.Note: these conditions are stronger than simply having a subset of size
 but rather applies to any pair of columns in a matrix. Therefore no matter what column
but rather applies to any pair of columns in a matrix. Therefore no matter what column 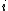 that is chosen in the matrix, that column will contain at least
that is chosen in the matrix, that column will contain at least  1's and the total number of shared 1's by any two columns is
1's and the total number of shared 1's by any two columns is  .
.Proof of Lemma 2: Fix an arbitrary
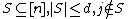 and a matrix
and a matrix 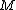 . There exists a match between
. There exists a match between 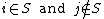 if column
if column 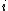 has a 1 in the same row position as in column
has a 1 in the same row position as in column 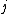 . Then the total number of matches is
. Then the total number of matches is  , i.e. a column
, i.e. a column 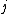 has a fewer number of matches than the number of ones in it. Therefore there must be a row with all 0s in
has a fewer number of matches than the number of ones in it. Therefore there must be a row with all 0s in 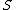 but a 1 in
but a 1 in 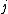 .
. 
We will now generate constructions for the bounds.
Randomized construction
This first construction will use a probabilistic argument to show the property wanted, in particular the Chernoff boundChernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
. Using this randomized construction gives that
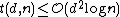 . The following lemma will give the result needed.
. The following lemma will give the result needed.Theorem 1: There exists a random
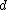 -disjunct matrix with
-disjunct matrix with  rows.
rows.Proof of Theorem 1: Begin by building a random
 matrix
matrix 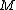 with
with 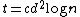 (where
(where  will be picked later). It will be shown that
will be picked later). It will be shown that 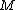 is
is 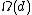 -disjunct. First note that
-disjunct. First note that 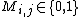 and let
and let  independently with probability
independently with probability 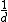 for
for 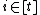 and
and 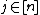 . Now fix
. Now fix 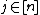 . Denote the
. Denote the 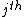 column of
column of  as
as  . Then the expectancy is
. Then the expectancy is 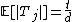 . Using the Chernoff bound, with
. Using the Chernoff bound, with 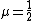 , gives
, gives 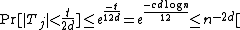 if
if 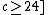 . Taking the union bound
. Taking the union boundBoole's inequality
In probability theory, Boole's inequality, also known as the union bound, says that for any finite or countable set of events, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events...
over all columns gives
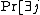 ,
, 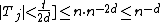 . This gives
. This gives  ,
,  . Therefore
. Therefore 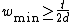 with probability
with probability  .
.Now suppose
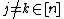 and
and 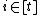 then
then 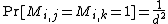 . So
. So 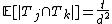 . Using the Chernoff bound on this gives
. Using the Chernoff bound on this gives  if
if  . By the union bound over
. By the union bound over 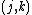 pairs
pairs 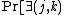 such that
such that  . This gives that
. This gives that 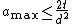 and
and 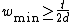 with probability
with probability 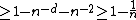 . Note that by changing
. Note that by changing  the probability
the probability 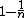 can be made to be
can be made to be 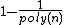 . Thus
. Thus 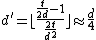 . By setting
. By setting 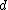 to be
to be  , the above argument shows that
, the above argument shows that 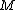 is
is 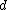 -disjunct.
-disjunct.Note that in this proof
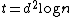 thus giving the upper bound of
thus giving the upper bound of 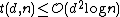 .
. 
Strongly explicit construction
It is possible to prove a bound of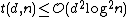 using a strongly explicit code. Although this bound is worse by a
using a strongly explicit code. Although this bound is worse by a 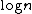 factor it is preferable because this produces a strongly explicit construction instead of a randomized one.
factor it is preferable because this produces a strongly explicit construction instead of a randomized one.Theorem 2: There exists a strongly explicit
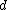 -disjunct matrix with
-disjunct matrix with 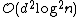 rows.
rows.This proof will use the properties of concatenated codes along with the properties of disjunct matrices to construct a code that will satisfy the bound we are after.
Proof of Theorem 2:
Let
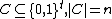 such that
such that 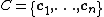 . Denote
. Denote 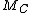 as the matrix with its
as the matrix with its 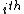 column being
column being 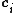 . If
. If 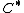 can be found such that
can be found such that
-
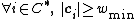
-
 ,
,
then
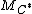 is
is  -disjunct. To complete the proof another concept must be introduced. This concept uses code concatenation to obtain the result we want.
-disjunct. To complete the proof another concept must be introduced. This concept uses code concatenation to obtain the result we want.Kautz-Singleton '64
Let
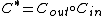 . Let
. Let 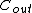 be a
be a  -Reed–Solomon code. Let
-Reed–Solomon code. Let  such that for
such that for 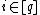 ,
, 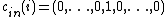 where the 1 is in the
where the 1 is in the 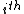 position. Then
position. Then  ,
, 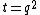 , and
, and 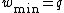 .
.---
Example: Let
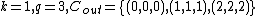 . Below,
. Below, 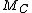 denotes the matrix of codewords for
denotes the matrix of codewords for 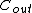 and
and 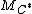 denotes the matrix of codewords for
denotes the matrix of codewords for 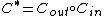 , where each column is a codeword. The overall image shows the transition from the outer code to the concatenated code.
, where each column is a codeword. The overall image shows the transition from the outer code to the concatenated code.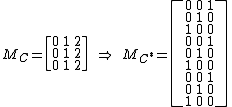
---
Divide the rows of
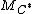 into sets of size
into sets of size 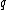 and number them as
and number them as 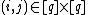 where
where 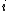 indexes the set of rows and
indexes the set of rows and 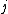 indexes the row in the set. If
indexes the row in the set. If 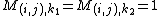 then note that
then note that 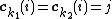 where
where 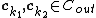 . So that means
. So that means 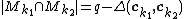 . Since
. Since 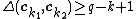 it gives that
it gives that 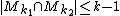 so let
so let 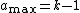 . Since
. Since  , the entries in each column of
, the entries in each column of 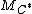 can be looked at as
can be looked at as 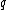 sets of
sets of  entries where only one of the entries is nonzero (by definition of
entries where only one of the entries is nonzero (by definition of 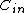 ) which gives a total of
) which gives a total of 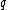 nonzero entries in each column. Therefore
nonzero entries in each column. Therefore 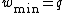 and
and 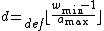 (so
(so 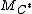 is
is  -disjunct).
-disjunct).Now pick
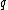 and
and 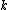 such that
such that  (so
(so 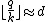 ). Since
). Since 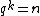 we have
we have 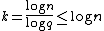 . Since
. Since 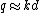 and
and 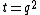 it gives that
it gives that 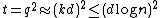 .
. 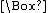
Thus we have a strongly explicit construction for a code that can be used to form a group testing matrix and so
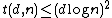 .
.For non-adaptive testing we have shown that
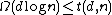 and we have that (i)
and we have that (i) 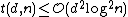 (strongly explicit) and (ii)
(strongly explicit) and (ii) 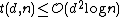 (randomized). As of recent work by Porat and Rothscheld they presented a explicit method construction (i.e. deterministic time but not strongly explicit) for
(randomized). As of recent work by Porat and Rothscheld they presented a explicit method construction (i.e. deterministic time but not strongly explicit) for 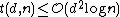 , however it is not shown here. There is also a lower bound for disjunct matrices of
, however it is not shown here. There is also a lower bound for disjunct matrices of 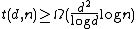 which is not shown here either.
which is not shown here either.