
Deriving the volume of an n-ball
Encyclopedia
In geometry
, the volume of a sphere
is a special case of the n-dimensional volume of a ball in n-dimensional Euclidean space.
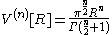
where Γ is the gamma function
. Because the proof for the volume of an n-ball depends upon the volume of an (n − 2)-ball there are two base cases, zero dimensions and one dimension.
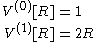
These are consistent with the desired formula because and
and 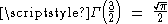 .
.
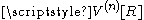 by assuming that we have already proved that
by assuming that we have already proved that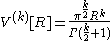
for k < n dimensions. We prove the formula using integration in polar coordinates: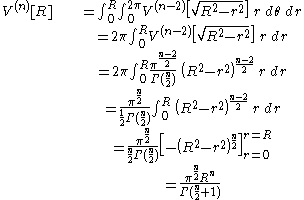
QED.
In particular, the volume formula for an n-ball can be reconstructed from the base cases and the recursion
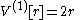
because this is just a line segment twice as long as the radius; i.e.,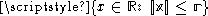 .
.
For n ≥ 1, we have: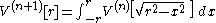

Then: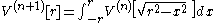
Now, here the fly is definitely in the ointment. Let's see what we can do.
Now we have established that for all n ≥ 1, the volume of an n-ball is proportional to the nth power of its radius; that is, if we denote the volume of the unit n-ball by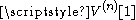 , we have:
, we have: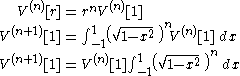
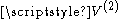 we have
we have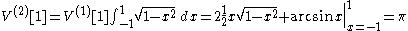
which is the area of the unit circle, as we expect. The next derivation, the volume of the unit sphere, is much easier:

Here is a graph of the integrand to make it easier to visualize what is going on:
By a change of variables u = 1 − x2 we have: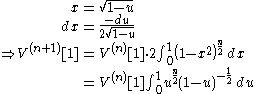
The integral on the far right is known as the beta function: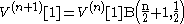
which can be expressed in terms of the gamma function
: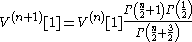
Since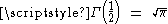 , we can easily verify by induction
, we can easily verify by induction
that for all n ≥ 1: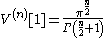
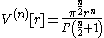
then its "surface area" is
This is an example of a disintegration of measure in Euclidean space.
and coding theory
. Also, since the expressions are analytical for complex (continuous) n, they are used in dimensional regularization
, a fundamental step in calculations within the standard model
of elementary particles.
In fact, for the unit Lp balls, we have the recurrence relation
from which one may recover the formula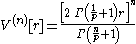
for the volume of a ball of radius r in , the volume measure being, as before, that of Lebesgue in the orthonormal (cartesian) coordinates. However, when p ≠ 2, it is no longer possible to calculate the (hyper)surface area by differentiating the volume of the ball with respect to its radius, because the radius is no longer everywhere normal to the surface.
, the volume measure being, as before, that of Lebesgue in the orthonormal (cartesian) coordinates. However, when p ≠ 2, it is no longer possible to calculate the (hyper)surface area by differentiating the volume of the ball with respect to its radius, because the radius is no longer everywhere normal to the surface.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the volume of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is a special case of the n-dimensional volume of a ball in n-dimensional Euclidean space.
Derivation of the volume of an n-ball
With a proof by induction, we calculate the volume of an n-ball of radius R to be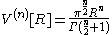
where Γ is the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. Because the proof for the volume of an n-ball depends upon the volume of an (n − 2)-ball there are two base cases, zero dimensions and one dimension.
Base cases
In zero dimensions a 0-ball is defined to be just one point, with a 0-volume of 1. In one dimension, the 1-ball of radius R is defined to be the interval [−R, R] and has 1-volume (length) of 2R.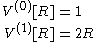
These are consistent with the desired formula because
 and
and 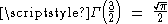 .
.General case
For the inductive argument, we will prove the formula for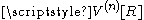 by assuming that we have already proved that
by assuming that we have already proved that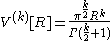
for k < n dimensions. We prove the formula using integration in polar coordinates:
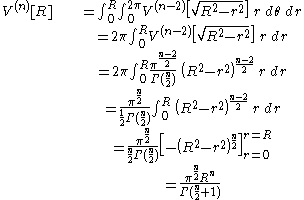
QED.
In particular, the volume formula for an n-ball can be reconstructed from the base cases and the recursion

General formula (recursive form)
Denote by V(n)[r] the volume of the n-ball of radius r. Then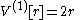
because this is just a line segment twice as long as the radius; i.e.,
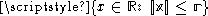 .
.For n ≥ 1, we have:
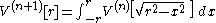
Volume is proportional to nth power of radius
We shall first show by induction that the volume of an n-ball is proportional to the nth power of its radius. We have already noted that this is true in one dimension. Suppose it is true for n dimensions; i.e.,:
Then:
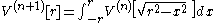
Now, here the fly is definitely in the ointment. Let's see what we can do.

Now we have established that for all n ≥ 1, the volume of an n-ball is proportional to the nth power of its radius; that is, if we denote the volume of the unit n-ball by
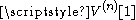 , we have:
, we have: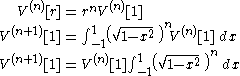
First few steps
In the case of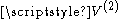 we have
we have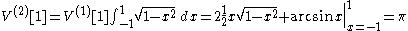
which is the area of the unit circle, as we expect. The next derivation, the volume of the unit sphere, is much easier:

General case
Let us try to generalize this derivation for a ball of any dimension:
Here is a graph of the integrand to make it easier to visualize what is going on:
By a change of variables u = 1 − x2 we have:
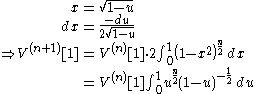
The integral on the far right is known as the beta function:
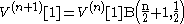
which can be expressed in terms of the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
:
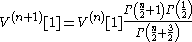
Since
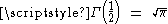 , we can easily verify by induction
, we can easily verify by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
that for all n ≥ 1:
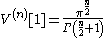
General form and surface area
The "surface area" of the n-ball (i.e., the (n − 1)-dimensional volume measure of the (n − 1)-sphere) can easily be found by differentiating the volume of the n-ball with respect to the radius. So, if we denote the volume of the n-ball of radius r by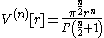
then its "surface area" is

This is an example of a disintegration of measure in Euclidean space.
Further generalizations
The alternative method of integration can carry over to balls in other Lp spaces where p ≠ 2, which has significance for information theoryInformation theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
. Also, since the expressions are analytical for complex (continuous) n, they are used in dimensional regularization
Dimensional regularization
In theoretical physics, dimensional regularization is a method introduced by Giambiagi and Bollini for regularizing integrals in the evaluation of Feynman diagrams; in other words, assigning values to them that are meromorphic functions of an auxiliary complex parameter d, called the...
, a fundamental step in calculations within the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of elementary particles.
In fact, for the unit Lp balls, we have the recurrence relation

from which one may recover the formula
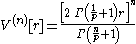
for the volume of a ball of radius r in
 , the volume measure being, as before, that of Lebesgue in the orthonormal (cartesian) coordinates. However, when p ≠ 2, it is no longer possible to calculate the (hyper)surface area by differentiating the volume of the ball with respect to its radius, because the radius is no longer everywhere normal to the surface.
, the volume measure being, as before, that of Lebesgue in the orthonormal (cartesian) coordinates. However, when p ≠ 2, it is no longer possible to calculate the (hyper)surface area by differentiating the volume of the ball with respect to its radius, because the radius is no longer everywhere normal to the surface.External links
- http://www.brouty.fr/Maths/sphere.html (derivation in hyperspherical coordinates.)
- http://mathworld.wolfram.com/Hypersphere.html
- http://www-staff.lboro.ac.uk/~coael/hypersphere.pdf
- http://www.mathreference.com/ca-int,hsp.html

