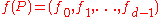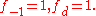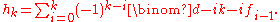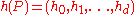Dehn-Sommerville equations
Encyclopedia
In mathematics, the Dehn–Sommerville equations are a complete set of linear relations between the numbers of faces of different dimension of a simplicial polytope
. For polytopes of dimension 4 and 5, they were found by Max Dehn
in 1905. Their general form was established by Duncan Sommerville
in 1927. The Dehn–Sommerville equations can be restated as a symmetry condition for the h-vector
of the simplicial polytope and this has become the standard formulation in recent combinatorics literature. By duality, analogous equations hold for simple polytope
s.
. For i = 0, 1, ..., d−1, let fi denote the number of i-dimensional faces
of P. The sequence
is called the f-vector of the polytope P. Additionally, set
Then for any k = −1, 0, …, d−2, the following Dehn–Sommerville equation holds:
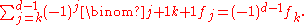
When k = −1, it expresses the fact that Euler characteristic
of a (d − 1)-dimensional simplicial sphere is equal to 1 + (−1)d−1.
Dehn–Sommerville equations with different k are not independent. There are several ways to choose a maximal independent subset consisting of
equations. If d is even then the equations with k = 0, 2, 4, …, d−2 are independent. Another independent set consists of the equations with k = −1, 1, 3, …, d−3. If d is odd then the equations with k = −1, 1, 3, …, d−2 form one independent set and the equations with k = −1, 0, 2, 4, …, d−3 form another.
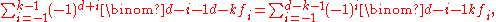
where 0 ≤ k ≤ ½(d−1). This can be further facilitated introducing the notion of h-vector of P. For k = 0, 1, …, d, let
The sequence
is called the h-vector
of P. The f-vector and the h-vector uniquely determine each other through the relation
Then the Dehn–Sommerville equations can be restated simply as
The equations with 0 ≤ k ≤ ½(d−1) are independent, and the others are manifestly equivalent to them.
Richard Stanley
gave an interpretation of the components of the h-vector of a simplicial convex polytope P in terms of the projective toric variety X associated with (the dual of) P. Namely, they are the dimensions of the even intersection cohomology
groups of X:
(the odd intersection cohomology
groups of X are all zero). In this language, the last form of the Dehn–Sommerville equations, the symmetry of the h-vector, is a manifestation of the Poincaré duality
in the intersection cohomology of X.
Simplicial polytope
In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
. For polytopes of dimension 4 and 5, they were found by Max Dehn
Max Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
in 1905. Their general form was established by Duncan Sommerville
Duncan MacLaren Young Sommerville
Duncan MacLaren Young Sommerville was a Scottish mathematician and astronomer, best known for his work in multidimensional geometry...
in 1927. The Dehn–Sommerville equations can be restated as a symmetry condition for the h-vector
H-vector
In algebraic combinatorics, the h-vector of a simplicial polytope is a fundamental invariant of the polytope which encodes the number of faces of different dimensions and allows one to express the Dehn–Sommerville equations in a particularly simple form...
of the simplicial polytope and this has become the standard formulation in recent combinatorics literature. By duality, analogous equations hold for simple polytope
Simple polytope
In geometry, a d-dimensional simple polytope is a d-dimensional polytope each of whose vertices are adjacent to exactly d edges . The vertex figure of a simple d-polytope is a -simplex....
s.
Statement
Let P be a d-dimensional simplicial polytopeSimplicial polytope
In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
. For i = 0, 1, ..., d−1, let fi denote the number of i-dimensional faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
of P. The sequence
is called the f-vector of the polytope P. Additionally, set
Then for any k = −1, 0, …, d−2, the following Dehn–Sommerville equation holds:
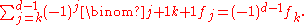
When k = −1, it expresses the fact that Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of a (d − 1)-dimensional simplicial sphere is equal to 1 + (−1)d−1.
Dehn–Sommerville equations with different k are not independent. There are several ways to choose a maximal independent subset consisting of
equations. If d is even then the equations with k = 0, 2, 4, …, d−2 are independent. Another independent set consists of the equations with k = −1, 1, 3, …, d−3. If d is odd then the equations with k = −1, 1, 3, …, d−2 form one independent set and the equations with k = −1, 0, 2, 4, …, d−3 form another.Equivalent formulations
Sommerville found a different way to state these equations: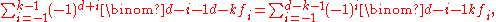where 0 ≤ k ≤ ½(d−1). This can be further facilitated introducing the notion of h-vector of P. For k = 0, 1, …, d, let
The sequence
is called the h-vector
H-vector
In algebraic combinatorics, the h-vector of a simplicial polytope is a fundamental invariant of the polytope which encodes the number of faces of different dimensions and allows one to express the Dehn–Sommerville equations in a particularly simple form...
of P. The f-vector and the h-vector uniquely determine each other through the relation
Then the Dehn–Sommerville equations can be restated simply as
The equations with 0 ≤ k ≤ ½(d−1) are independent, and the others are manifestly equivalent to them.
Richard Stanley
Richard P. Stanley
Richard Peter Stanley is the Norman Levinson Professor of Applied Mathematics at the Massachusetts Institute of Technology, in Cambridge, Massachusetts. He received his Ph.D. at Harvard University in 1971 under the supervision of Gian-Carlo Rota...
gave an interpretation of the components of the h-vector of a simplicial convex polytope P in terms of the projective toric variety X associated with (the dual of) P. Namely, they are the dimensions of the even intersection cohomology
Intersection cohomology
In topology, a branch of mathematics, intersection homology is an analogue of singular homology especially well-suited for the study of singular spaces, discovered by Mark Goresky and Robert MacPherson in the fall of 1974 and developed by them over the next few years.Intersection cohomology was...
groups of X:
(the odd intersection cohomology
Intersection cohomology
In topology, a branch of mathematics, intersection homology is an analogue of singular homology especially well-suited for the study of singular spaces, discovered by Mark Goresky and Robert MacPherson in the fall of 1974 and developed by them over the next few years.Intersection cohomology was...
groups of X are all zero). In this language, the last form of the Dehn–Sommerville equations, the symmetry of the h-vector, is a manifestation of the Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
in the intersection cohomology of X.