
Decision-theoretic rough sets
Encyclopedia
Decision-theoretic rough sets (DTRS) is a probabilistic extension of rough set
classification. First created in 1990 by Dr. Yiyu Yao, the extension makes use of loss functions to derive and
and 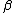 region parameters. Like rough sets, the lower and upper approximations of a set are used.
region parameters. Like rough sets, the lower and upper approximations of a set are used.
risk decision making based on observed evidence. Let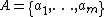 be a finite set of
be a finite set of 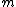
possible actions and let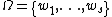 be a finite set of
be a finite set of  states.
states. 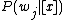 is
is
calculated as the conditional probability of an object being in state
being in state 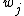 given the object description
given the object description
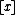 .
. 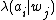 denotes the loss, or cost, for performing action
denotes the loss, or cost, for performing action 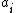 when the state is
when the state is 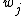 .
.
The expected loss (conditional risk) associated with taking action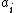 is given
is given
by:
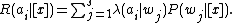
Object classification with the approximation operators can be fitted into the Bayesian decision framework. The
set of actions is given by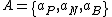 , where
, where 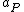 ,
, 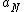 , and
, and 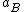 represent the three
represent the three
actions in classifying an object into POS(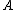 ), NEG(
), NEG(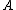 ), and BND(
), and BND(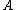 ) respectively. To indicate whether an
) respectively. To indicate whether an
element is in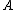 or not in
or not in 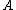 , the set of states is given by
, the set of states is given by 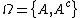 . Let
. Let
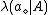 denote the loss incurred by taking action
denote the loss incurred by taking action 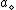 when an object belongs to
when an object belongs to
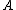 , and let
, and let 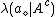 denote the loss incurred by take the same action when the object
denote the loss incurred by take the same action when the object
belongs to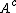 .
.
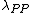 denote the loss function for classifying an object in
denote the loss function for classifying an object in  into the POS region,
into the POS region, 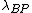 denote the loss function for classifying an object in
denote the loss function for classifying an object in 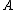 into the BND region, and let
into the BND region, and let  denote the loss function for classifying an object in
denote the loss function for classifying an object in 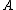 into the NEG region. A loss function
into the NEG region. A loss function 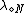 denotes the loss of classifying an object that does not belong to
denotes the loss of classifying an object that does not belong to 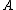 into the regions specified by
into the regions specified by  .
.
Taking individual can be associated with the expected loss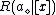 actions and can be expressed as:
actions and can be expressed as:
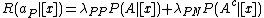 ,
,
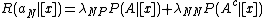 ,
,
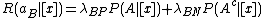 ,
,
where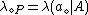 ,
, 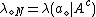 , and
, and  ,
,  , or
, or 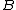 .
.
 and
and  , the following decision rules are formulated (P, N, B):
, the following decision rules are formulated (P, N, B):
where,
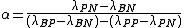 ,
,
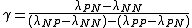 ,
,
 .
.
The ,
, 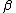 , and
, and 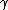 values define the three different regions, giving us an associated risk for classifying an object. When
values define the three different regions, giving us an associated risk for classifying an object. When 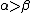 , we get
, we get 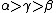 and can simplify (P, N, B) into (P1, N1, B1):
and can simplify (P, N, B) into (P1, N1, B1):
When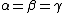 , we can simplify the rules (P-B) into (P2-B2), which divide the regions based solely on
, we can simplify the rules (P-B) into (P2-B2), which divide the regions based solely on  :
:
Data mining
, feature selection
, information retrieval
, and classifications are just some of the applications in which the DTRS approach has been successfully used.
Rough set
In computer science, a rough set, first described by a Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set in terms of a pair of sets which give the lower and the upper approximation of the original set...
classification. First created in 1990 by Dr. Yiyu Yao, the extension makes use of loss functions to derive
 and
and 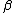 region parameters. Like rough sets, the lower and upper approximations of a set are used.
region parameters. Like rough sets, the lower and upper approximations of a set are used.Conditional Risk
Using the Bayesian decision procedure, the decision-theoretic rough set (DTRS) approach allows for minimumrisk decision making based on observed evidence. Let
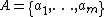 be a finite set of
be a finite set of 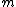
possible actions and let
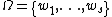 be a finite set of
be a finite set of  states.
states. 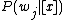 is
iscalculated as the conditional probability of an object
 being in state
being in state 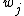 given the object description
given the object description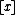 .
. 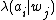 denotes the loss, or cost, for performing action
denotes the loss, or cost, for performing action 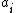 when the state is
when the state is 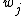 .
.The expected loss (conditional risk) associated with taking action
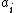 is given
is givenby:
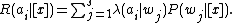
Object classification with the approximation operators can be fitted into the Bayesian decision framework. The
set of actions is given by
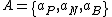 , where
, where 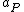 ,
, 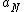 , and
, and 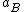 represent the three
represent the threeactions in classifying an object into POS(
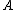 ), NEG(
), NEG(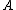 ), and BND(
), and BND(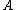 ) respectively. To indicate whether an
) respectively. To indicate whether anelement is in
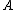 or not in
or not in 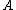 , the set of states is given by
, the set of states is given by 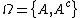 . Let
. Let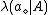 denote the loss incurred by taking action
denote the loss incurred by taking action 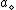 when an object belongs to
when an object belongs to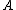 , and let
, and let 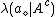 denote the loss incurred by take the same action when the object
denote the loss incurred by take the same action when the objectbelongs to
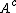 .
.Loss Functions
Let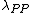 denote the loss function for classifying an object in
denote the loss function for classifying an object in  into the POS region,
into the POS region, 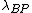 denote the loss function for classifying an object in
denote the loss function for classifying an object in 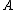 into the BND region, and let
into the BND region, and let  denote the loss function for classifying an object in
denote the loss function for classifying an object in 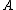 into the NEG region. A loss function
into the NEG region. A loss function 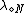 denotes the loss of classifying an object that does not belong to
denotes the loss of classifying an object that does not belong to 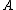 into the regions specified by
into the regions specified by  .
.Taking individual can be associated with the expected loss
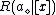 actions and can be expressed as:
actions and can be expressed as: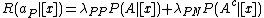 ,
,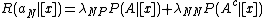 ,
,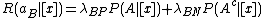 ,
,where
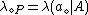 ,
, 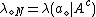 , and
, and 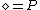 ,
,  , or
, or 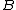 .
.Minimum Risk Decision Rules
If we consider the loss functions and
and  , the following decision rules are formulated (P, N, B):
, the following decision rules are formulated (P, N, B):- P: If
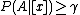 and
and 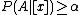 , decide POS(
, decide POS( );
); - N: If
 and
and 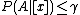 , decide NEG(
, decide NEG( );
); - B: If
 , decide BND(
, decide BND( );
);
where,
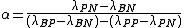 ,
,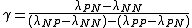 ,
, .
.The
 ,
, 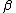 , and
, and 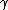 values define the three different regions, giving us an associated risk for classifying an object. When
values define the three different regions, giving us an associated risk for classifying an object. When 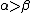 , we get
, we get 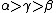 and can simplify (P, N, B) into (P1, N1, B1):
and can simplify (P, N, B) into (P1, N1, B1):- P1: If
 , decide POS(
, decide POS(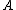 );
); - N1: If
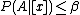 , decide NEG(
, decide NEG(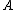 );
); - B1: If
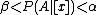 , decide BND(
, decide BND(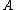 ).
).
When
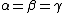 , we can simplify the rules (P-B) into (P2-B2), which divide the regions based solely on
, we can simplify the rules (P-B) into (P2-B2), which divide the regions based solely on  :
:- P2: If
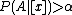 , decide POS(
, decide POS(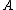 );
); - N2: If
 , decide NEG(
, decide NEG(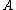 );
); - B2: If
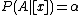 , decide BND(
, decide BND( ).
).
Data mining
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
, feature selection
Feature selection
In machine learning and statistics, feature selection, also known as variable selection, feature reduction, attribute selection or variable subset selection, is the technique of selecting a subset of relevant features for building robust learning models...
, information retrieval
Information retrieval
Information retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
, and classifications are just some of the applications in which the DTRS approach has been successfully used.

