DNSS point
Encyclopedia
DNSS points arise in optimal control
problems that exhibit multiple optimal solutions. A DNSS point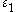
named alphabetically after Deckert and Nishimura, Sethi, and Skiba
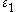is an indifference point in an optimal control problem such that starting from such a point, the problem has more than one different optimal solutions. A good discussion of such points can be found in Grass et al.
problems that are autonomous. These problems can be formulated as
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
problems that exhibit multiple optimal solutions. A DNSS point
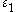named alphabetically after Deckert and Nishimura, Sethi, and Skiba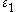is an indifference point in an optimal control problem such that starting from such a point, the problem has more than one different optimal solutions. A good discussion of such points can be found in Grass et al.Definition
Of particular interest here are discounted infinite horizon optimal controlOptimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
problems that are autonomous. These problems can be formulated as
-
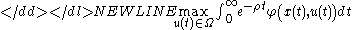
s.t.
-
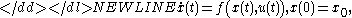
where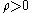
is the discount rate, 
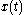and 
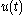are the state and control variables, respectively, at time 
, functions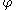 
and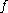 
are assumed to be continuously differentiable with respect to their arguments and they do not depend explicitly on time 
, and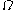 
is the set of feasible controls and it also is explicitly independent of time 
. Furthermore, it is assumed that the integral converges for any admissible solution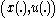 
. In such a problem with one-dimensional state variable 
, the initial state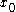 
is called a DNSS point if the system starting from it exhibits multiple optimal solutions or equilibria. Thus, at least in the neighborhood of 
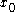, the system moves to one equilibrium for 
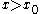and to another for 
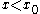. In this sense, 
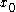is an indifference point from which the system could move to either of the two equilibria.
For two-dimensional optimal controlOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
problems, Grass et al. and Zeiler et al. present examples that exhibit DNSS curves.
Some references on the application of DNSS points are Caulkins et al. and Zeiler et al.
History
Suresh P. SethiSuresh P. SethiSuresh P. Sethi is Charles & Nancy Davidson Distinguished Professor of Operations Management and Director of the Center for Intelligent Supply Networks at The University of Texas at Dallas. He has contributed significantly in the fields of manufacturing and operations management, finance and...
identified such indifference points for the first time in 1977. Further, Skiba, Sethi, and Deckert and Nishimura explored these indifference points in economic models. The term DNSS (Deckert, Nishimura, Sethi, Skiba) points, introduced by Grass et al., recognizes (alphabetically) the contributions of these authors.
These indifference points have been referred to earlier as Skiba points or DNS points in the literature.
Example
A simple problem exhibiting this behavior is given by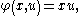
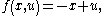and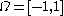 
. It is shown in Grass et al. that 
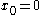is a DNSS point for this problem because the optimal path 
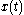can be either 
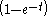or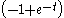 
. Note that for 
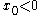, the optimal path is 
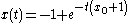and for 
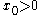, the optimal path is 
.
-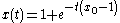