
D'Alembert's formula
Encyclopedia
In mathematics
, and specifically partial differential equations, d´Alembert's formula is the general solution to the one-dimensional wave equation
: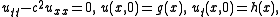
for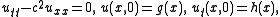 . It is named after the mathematician Jean le Rond d'Alembert
. It is named after the mathematician Jean le Rond d'Alembert
.
The characteristics
of the PDE are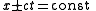 , so use the change of variables
, so use the change of variables 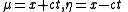 to transform the PDE to
to transform the PDE to 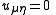 . The general solution of this PDE is
. The general solution of this PDE is 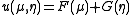 where
where 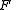 and
and 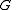 are
are 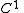 functions. Back in
functions. Back in 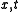 coordinates,
coordinates,

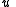 is
is  if
if 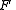 and
and 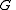 are
are 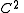 .
.
This solution can be interpreted as two waves with constant velocity
can be interpreted as two waves with constant velocity  moving in opposite directions along the x-axis.
moving in opposite directions along the x-axis.
Now consider this solution with the Cauchy data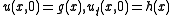 .
.
Using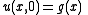 we get
we get 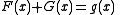 .
.
Using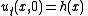 we get
we get 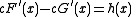 .
.
Integrate the last equation to get
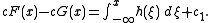
Now solve this system of equations to get
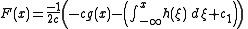
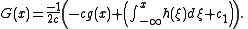
Now, using

d´Alembert's formula becomes:
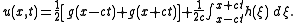
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and specifically partial differential equations, d´Alembert's formula is the general solution to the one-dimensional wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
:
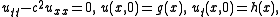
for
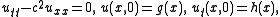 . It is named after the mathematician Jean le Rond d'Alembert
. It is named after the mathematician Jean le Rond d'AlembertJean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
.
The characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
of the PDE are
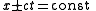 , so use the change of variables
, so use the change of variables 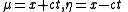 to transform the PDE to
to transform the PDE to 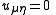 . The general solution of this PDE is
. The general solution of this PDE is 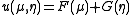 where
where 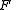 and
and 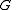 are
are 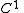 functions. Back in
functions. Back in 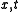 coordinates,
coordinates,
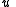 is
is  if
if 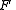 and
and 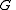 are
are 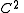 .
.This solution
 can be interpreted as two waves with constant velocity
can be interpreted as two waves with constant velocity  moving in opposite directions along the x-axis.
moving in opposite directions along the x-axis.Now consider this solution with the Cauchy data
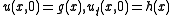 .
.Using
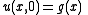 we get
we get 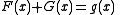 .
.Using
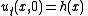 we get
we get 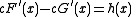 .
.Integrate the last equation to get
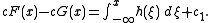
Now solve this system of equations to get
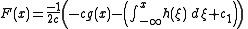
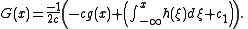
Now, using

d´Alembert's formula becomes:
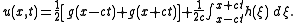
External links
- An example of solving a nonhomogeneous wave equation from www.exampleproblems.com

