Credible interval
Encyclopedia
In Bayesian statistics
, a credible interval (or Bayesian confidence interval) is an interval in the domain of a posterior probability distribution used for interval estimation
. The generalisation to multivariate problems is the credible region. Credible intervals are analogous to confidence interval
s in frequentist statistics.
For example, in an experiment that determines the uncertainty distribution of parameter
, if the probability that 
lies between 35 and 45 is 90%, then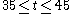 
is a 90% credible interval.
It is possible to frame the choice of a credible interval within decision theory
and, in that context, an optimal interval will always be a highest probability density set.
of 35–45 means that with a large number of repeated samples, 90% of the calculated confidence intervals would include the true value of the parameter. The probability that the parameter is inside the given interval (say, 35–45) is either 0 or 1 (the non-random unknown parameter is either there or not). In frequentist terms, the parameter is fixed (cannot be considered to have a distribution of possible values) and the confidence interval is random (as it depends on the random sample). Antelman (1997, p. 375) summarizes a confidence interval as "... one interval generated by a procedure that will give correct intervals 95 % [resp. 90 %] of the time".
In general, Bayesian credible intervals do not coincide with frequentist confidence intervals for two reasons:
For the case of a single parameter and data that can be summarised in a single sufficient statistic, it can be shown that the credible interval and the confidence interval will coincide if the unknown parameter is a location parameter
(i.e. the forward probability function has the form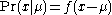
), with a prior that is a uniform flat distribution; and also if the unknown parameter is a scale parameter
(i.e. the forward probability function has the form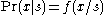
), with a Jeffreys' prior 
— the latter following because taking the logarithm of such a scale parameter turns it into a location parameter with a uniform distribution.
But these are distinctly special (albeit important) cases; in general no such equivalence can be made.
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
, a credible interval (or Bayesian confidence interval) is an interval in the domain of a posterior probability distribution used for interval estimation
Interval estimation
In statistics, interval estimation is the use of sample data to calculate an interval of possible values of an unknown population parameter, in contrast to point estimation, which is a single number. Neyman identified interval estimation as distinct from point estimation...
. The generalisation to multivariate problems is the credible region. Credible intervals are analogous to confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s in frequentist statistics.
For example, in an experiment that determines the uncertainty distribution of parameter
, if the probability that lies between 35 and 45 is 90%, then 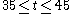is a 90% credible interval.Choosing a credible interval
Credible intervals are not unique on a posterior distribution. Methods for defining a suitable credible interval include:- Choosing the narrowest interval, which for a unimodal distribution will involve choosing those values of highest probability density including the modeMode (statistics)In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
. - Choosing the interval where the probability of being below the interval is as likely as being above it. This interval will include the median.
- Assuming the mean exists, choosing the interval for which the mean is the central point.
It is possible to frame the choice of a credible interval within decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
and, in that context, an optimal interval will always be a highest probability density set.
Contrasts with confidence interval
A frequentist 90% confidence intervalConfidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
of 35–45 means that with a large number of repeated samples, 90% of the calculated confidence intervals would include the true value of the parameter. The probability that the parameter is inside the given interval (say, 35–45) is either 0 or 1 (the non-random unknown parameter is either there or not). In frequentist terms, the parameter is fixed (cannot be considered to have a distribution of possible values) and the confidence interval is random (as it depends on the random sample). Antelman (1997, p. 375) summarizes a confidence interval as "... one interval generated by a procedure that will give correct intervals 95 % [resp. 90 %] of the time".
In general, Bayesian credible intervals do not coincide with frequentist confidence intervals for two reasons:
- credible intervals incorporate problem-specific contextual information from the prior distribution whereas confidence intervals are based only on the data;
- credible intervals and confidence intervals treat nuisance parameters in radically different ways.
For the case of a single parameter and data that can be summarised in a single sufficient statistic, it can be shown that the credible interval and the confidence interval will coincide if the unknown parameter is a location parameter
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
(i.e. the forward probability function has the form
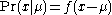), with a prior that is a uniform flat distribution; and also if the unknown parameter is a scale parameterScale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
(i.e. the forward probability function has the form
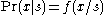), with a Jeffreys' prior — the latter following because taking the logarithm of such a scale parameter turns it into a location parameter with a uniform distribution.But these are distinctly special (albeit important) cases; in general no such equivalence can be made.