Correlation sum
Encyclopedia
In chaos theory
, the correlation sum is the estimator of the correlation integral, which reflects the mean probability that the states at two different times are close:
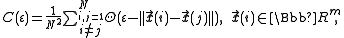
where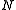
is the number of considered states 
, 
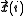is a threshold distance, 
a norm (e.g. Euclidean norm) and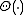 
the Heaviside step function
. If only a time series
is available, the phase space can be reconstructed by using a time delay embedding (see Takens' theorem
):
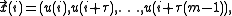
where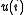
is the time series, 
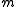the embedding dimension and 
the time delay.
The correlation sum is used to estimate the correlation dimension
.
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, the correlation sum is the estimator of the correlation integral, which reflects the mean probability that the states at two different times are close:
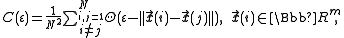
where
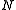is the number of considered states 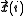, is a threshold distance, a norm (e.g. Euclidean norm) and 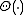the Heaviside step functionHeaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
. If only a time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
is available, the phase space can be reconstructed by using a time delay embedding (see Takens' theorem
Takens' theorem
In mathematics, a delay embedding theorem gives the conditions under which a chaotic dynamical system can be reconstructed from a sequence of observations of the state of a dynamical system...
):
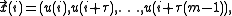
where
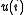is the time series, 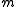the embedding dimension and the time delay.The correlation sum is used to estimate the correlation dimension
Correlation dimension
In chaos theory, the correlation dimension is a measure of the dimensionality of the space occupied by a set of random points, often referred to as a type of fractal dimension....
.
See also
- Correlation integral
- Correlation dimensionCorrelation dimensionIn chaos theory, the correlation dimension is a measure of the dimensionality of the space occupied by a set of random points, often referred to as a type of fractal dimension....
- Recurrence quantification analysisRecurrence quantification analysisRecurrence quantification analysis is a method of nonlinear data analysis for the investigation of dynamical systems. It quantifies the number and duration of recurrences of a dynamical system presented by its phase space trajectory....