
Correction for attenuation
Encyclopedia
Correction for attenuation is a statistical procedure, due to Spearman
(1904), to "rid a correlation
coefficient from the weakening effect of measurement error" (Jensen, 1998), a phenomenon also known as regression dilution
. In measurement
and statistics
, it is also called disattenuation. The correlation
between two sets of parameters or measurements is the estimated a manner that accounts for measurement error contained within the estimates
of those parameters.
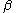 and
and 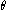 be the true values of two attributes of some person or statistical unit
be the true values of two attributes of some person or statistical unit
. These values are regarded as random variables by virtue of the statistical unit being selected randomly from some population
. Let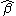 and
and 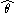 be estimates of
be estimates of 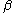 and
and 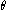 derived either directly by observation-with-error or from application of a measurement model, such as the Rasch model
derived either directly by observation-with-error or from application of a measurement model, such as the Rasch model
. Also, let
Charles Spearman
Charles Edward Spearman, FRS was an English psychologist known for work in statistics, as a pioneer of factor analysis, and for Spearman's rank correlation coefficient...
(1904), to "rid a correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
coefficient from the weakening effect of measurement error" (Jensen, 1998), a phenomenon also known as regression dilution
Regression dilution
Regression dilution is a statistical phenomenon also known as "attenuation".Consider fitting a straight line for the relationship of an outcome variable y to a predictor variable x, and estimating the gradient of the line...
. In measurement
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, it is also called disattenuation. The correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
between two sets of parameters or measurements is the estimated a manner that accounts for measurement error contained within the estimates
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of those parameters.
Background
Correlations between parameters are diluted or weakened by measurement error. Disattenuation provides for a more accurate estimate of the correlation between the parameters by accounting for this effect.Derivation of the formula
Let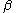 and
and 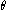 be the true values of two attributes of some person or statistical unit
be the true values of two attributes of some person or statistical unitStatistical unit
A unit in a statistical analysis refers to one member of a set of entities being studied. It is the material source for the mathematical abstraction of a "random variable"...
. These values are regarded as random variables by virtue of the statistical unit being selected randomly from some population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
. Let
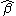 and
and 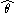 be estimates of
be estimates of 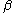 and
and 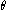 derived either directly by observation-with-error or from application of a measurement model, such as the Rasch model
derived either directly by observation-with-error or from application of a measurement model, such as the Rasch modelRasch model
Rasch models are used for analysing data from assessments to measure variables such as abilities, attitudes, and personality traits. For example, they may be used to estimate a student's reading ability from answers to questions on a reading assessment, or the extremity of a person's attitude to...
. Also, let
-
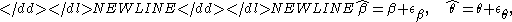
where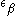 and
and  are the measurement errors associated with the estimates
are the measurement errors associated with the estimates  and
and 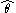 .
.
The correlation between two sets of estimates is
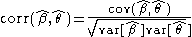
-
-
-
-
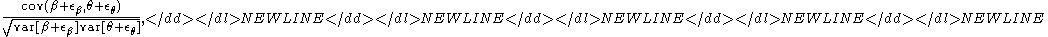
which, assuming the errors are uncorrelated with each other and with the estimates, gives
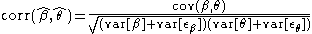
-
-
-
-

-
-
-
-

where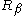 is the separation index of the set of estimates of
is the separation index of the set of estimates of 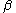 , which is analogous to Cronbach's alphaCronbach's alphaCronbach's \alpha is a coefficient of reliability. It is commonly used as a measure of the internal consistency or reliability of a psychometric test score for a sample of examinees. It was first named alpha by Lee Cronbach in 1951, as he had intended to continue with further coefficients...
, which is analogous to Cronbach's alphaCronbach's alphaCronbach's \alpha is a coefficient of reliability. It is commonly used as a measure of the internal consistency or reliability of a psychometric test score for a sample of examinees. It was first named alpha by Lee Cronbach in 1951, as he had intended to continue with further coefficients...
; this is, in terms of Classical test theoryClassical test theoryClassical test theory is a body of related psychometric theory that predict outcomes of psychological testing such as the difficulty of items or the ability of test-takers. Generally speaking, the aim of classical test theory is to understand and improve the reliability of psychological...
,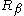 is analogous to a reliability coefficient. Specifically, the separation index is given as follows:
is analogous to a reliability coefficient. Specifically, the separation index is given as follows:
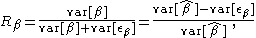
where the mean squared standard error of person estimate gives an estimate of the variance of the errors, . The standard errors are normally produced as a by-product of the estimation process (see Rasch model estimationRasch model estimationEstimation of a Rasch model is used to estimate the parameters of the Rasch model. Various techniques are employed to estimate the parameters from matrices of response data. The most common approaches are types of maximum likelihood estimation, such as joint and conditional maximum likelihood...
. The standard errors are normally produced as a by-product of the estimation process (see Rasch model estimationRasch model estimationEstimation of a Rasch model is used to estimate the parameters of the Rasch model. Various techniques are employed to estimate the parameters from matrices of response data. The most common approaches are types of maximum likelihood estimation, such as joint and conditional maximum likelihood...
).
The disattenuated estimate of the correlation between two sets of parameters or measures is therefore
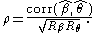
That is, the disattenuated correlation is obtained by dividing the correlation between the estimates by the square root of the product of the separation indices of the two sets of estimates. Expressed in terms of Classical test theory, the correlation is divided by the square root of the product of the reliability coefficients of two tests.
Given two random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s and
and  , with correlationCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
, with correlationCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
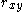 , and a known reliability for each variable,
, and a known reliability for each variable, 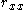 and
and 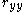 , the correlation between
, the correlation between  and
and  corrected for attenuation is
corrected for attenuation is
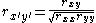 .
.
How well the variables are measured affects the correlation of X and Y. The correction for attenuation tells you what the correlation would be if you could measure X and Y with perfect reliability.
If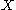 and
and  are taken to be imperfect measurements of underlying variables
are taken to be imperfect measurements of underlying variables 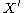 and
and 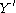 with independent errors, then
with independent errors, then 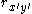 measures the true correlation between
measures the true correlation between 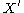 and
and  .
.
See also
- Regression dilutionRegression dilutionRegression dilution is a statistical phenomenon also known as "attenuation".Consider fitting a straight line for the relationship of an outcome variable y to a predictor variable x, and estimating the gradient of the line...
- Errors-in-variables modelErrors-in-variables modelTotal least squares, also known as errors in variables, rigorous least squares, or orthogonal regression, is a least squares data modeling technique in which observational errors on both dependent and independent variables are taken into account...
External links
- Regression dilution
-
-
-
-
-
-
-
-
-
-
-
-

