
Conway base 13 function
Encyclopedia
The Conway base 13 function is a function created by British
mathematician
John H. Conway as a counterexample to the converse of the intermediate value theorem
. In other words, even though Conway's function f is not continuous
, if f(a) < f(b) and an arbitrary value x is chosen such that f(a) < x < f(b), a point c lying between a and b can always be found such that f(c) = x.
, namely sin(1/x). This function is only discontinuous at one point (0) and seemed like a cheat to many. Conway's function, on the other hand, is discontinuous at every point.
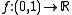 defined as follows.
defined as follows.
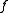 defined in this way satisfies the converse to the intermediate value theorem but is continuous nowhere. That is, on any closed interval
defined in this way satisfies the converse to the intermediate value theorem but is continuous nowhere. That is, on any closed interval  of the real line,
of the real line,  takes on every value between
takes on every value between 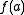 and
and 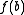 . Indeed,
. Indeed, 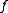 takes on the value of every real number on any closed interval
takes on the value of every real number on any closed interval 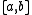 where b > a. To see this, note that we can take any number
where b > a. To see this, note that we can take any number  and modify the tail end of its base 13 expansion to be of the form
and modify the tail end of its base 13 expansion to be of the form  (the last three dots are not base 13 digits, but just indicate that the expansion continues), and we are free to make the
(the last three dots are not base 13 digits, but just indicate that the expansion continues), and we are free to make the 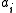 and
and 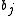 whatever we want while only slightly altering the value of
whatever we want while only slightly altering the value of  . We can do this in such a way that the new number we have created, call it
. We can do this in such a way that the new number we have created, call it  , still lies in the interval
, still lies in the interval 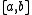 , but we have made
, but we have made  a real number of our choice. Thus
a real number of our choice. Thus 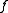 satisfies the converse to the intermediate value theorem (and then some). Moreover, if
satisfies the converse to the intermediate value theorem (and then some). Moreover, if  were continuous at some point,
were continuous at some point, 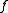 would be locally bounded at this point, which is not the case. Thus
would be locally bounded at this point, which is not the case. Thus  is a spectacular counterexample to the converse of the intermediate value theorem.
is a spectacular counterexample to the converse of the intermediate value theorem.
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
John H. Conway as a counterexample to the converse of the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
. In other words, even though Conway's function f is not continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, if f(a) < f(b) and an arbitrary value x is chosen such that f(a) < x < f(b), a point c lying between a and b can always be found such that f(c) = x.
Purpose
The Conway base 13 function was created in response to complaints about the standard counterexample to the converse of the intermediate value theoremIntermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
, namely sin(1/x). This function is only discontinuous at one point (0) and seemed like a cheat to many. Conway's function, on the other hand, is discontinuous at every point.
Definition
The Conway base 13 function is a function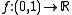 defined as follows.
defined as follows.
- If
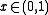 expand
expand  as a tredecimal (a "decimal" in base 13Base 13Base-13, tridecimal, tredecimal, or triskadecimal is a positional numeral system with thirteen as its base. It uses 13 different digits for representing numbers...
as a tredecimal (a "decimal" in base 13Base 13Base-13, tridecimal, tredecimal, or triskadecimal is a positional numeral system with thirteen as its base. It uses 13 different digits for representing numbers...
) using the symbols 0,1,2,3,4,5,6,7,8,9, ,-,+ (avoid + recurring).
,-,+ (avoid + recurring). - Define
 unless the expansion ends with:
unless the expansion ends with:
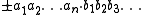 (Note: Here the symbols "+" and "-" are used as symbols of base 13 decimal expansion, and do not have the usual meaning of the plus and minus sign; the
(Note: Here the symbols "+" and "-" are used as symbols of base 13 decimal expansion, and do not have the usual meaning of the plus and minus sign; the 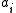 s and
s and 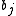 s are restricted to the digits 0,1,2,...,9).
s are restricted to the digits 0,1,2,...,9).
- In this case define
 read in decimal (here we use the conventional definitions of the "+" and "-" symbols, and "
read in decimal (here we use the conventional definitions of the "+" and "-" symbols, and " " is interpreted as a decimal point).
" is interpreted as a decimal point).
Properties
The important thing to note is that the function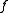 defined in this way satisfies the converse to the intermediate value theorem but is continuous nowhere. That is, on any closed interval
defined in this way satisfies the converse to the intermediate value theorem but is continuous nowhere. That is, on any closed interval  of the real line,
of the real line,  takes on every value between
takes on every value between 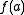 and
and 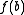 . Indeed,
. Indeed, 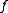 takes on the value of every real number on any closed interval
takes on the value of every real number on any closed interval 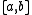 where b > a. To see this, note that we can take any number
where b > a. To see this, note that we can take any number  and modify the tail end of its base 13 expansion to be of the form
and modify the tail end of its base 13 expansion to be of the form  (the last three dots are not base 13 digits, but just indicate that the expansion continues), and we are free to make the
(the last three dots are not base 13 digits, but just indicate that the expansion continues), and we are free to make the 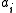 and
and 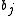 whatever we want while only slightly altering the value of
whatever we want while only slightly altering the value of  . We can do this in such a way that the new number we have created, call it
. We can do this in such a way that the new number we have created, call it  , still lies in the interval
, still lies in the interval 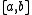 , but we have made
, but we have made  a real number of our choice. Thus
a real number of our choice. Thus 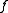 satisfies the converse to the intermediate value theorem (and then some). Moreover, if
satisfies the converse to the intermediate value theorem (and then some). Moreover, if  were continuous at some point,
were continuous at some point, 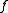 would be locally bounded at this point, which is not the case. Thus
would be locally bounded at this point, which is not the case. Thus  is a spectacular counterexample to the converse of the intermediate value theorem.
is a spectacular counterexample to the converse of the intermediate value theorem.

