
Convex preferences
Encyclopedia
In economics
, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes". The concept roughly corresponds to the "law" of diminishing marginal utility but uses modern theory to represent the concept without requiring the use of utility functions.
Comparable to the greater-than-or-equal-to ordering relation for real numbers, the notation
for real numbers, the notation  below can be translated as: 'is at least as good as' (in preference
below can be translated as: 'is at least as good as' (in preference
satisfaction). Use x, y, and z to denote three consumption bundles (combinations of various quantities of various goods). Formally, a preference relation P on the consumption set X is convex
if for any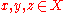 where
where  and
and  ,
,
it is the case that for any
for any  .
.
That is, the preference ordering P is convex if for any two goods bundles that are each viewed as being at least as good as a third bundle, a weighted average of the two bundles is also viewed as being at least as good as the third bundle.
Moreover,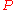 is strictly convex if for any
is strictly convex if for any where
where  ,
,  , and
, and  ,
,
it is also true that for any
for any 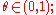
here can be translated as 'is better than' (in preference satisfaction). Thus the preference ordering P is strictly convex if for any two distinct goods bundles that are each viewed as being at least as good as a third bundle, a weighted average of the two bundles (including a positive amount of each bundle) is viewed as being better than the third bundle.
can be translated as 'is better than' (in preference satisfaction). Thus the preference ordering P is strictly convex if for any two distinct goods bundles that are each viewed as being at least as good as a third bundle, a weighted average of the two bundles (including a positive amount of each bundle) is viewed as being better than the third bundle.
A set of convex
-shaped indifference curve
s displays convex preferences: Given a convex indifference curve containing the set of all bundles (of two or more goods) that are all viewed as equally desired, the set of all goods bundles that are viewed as being at least as desired as those on the indifference curve is a convex set
.
Convex preferences with their associated convex indifference mapping arise from quasi-concave utility functions, although these are not necessary for the analysis of preferences.
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes". The concept roughly corresponds to the "law" of diminishing marginal utility but uses modern theory to represent the concept without requiring the use of utility functions.
Comparable to the greater-than-or-equal-to ordering relation
 for real numbers, the notation
for real numbers, the notation  below can be translated as: 'is at least as good as' (in preference
below can be translated as: 'is at least as good as' (in preferencePreference (economics)
In economics and other social sciences, preference refers to the set of assumptions related to ordering some alternatives, based on the degree of happiness, satisfaction, gratification, enjoyment, or utility they provide, a process which results in an optimal "choice"...
satisfaction). Use x, y, and z to denote three consumption bundles (combinations of various quantities of various goods). Formally, a preference relation P on the consumption set X is convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
if for any
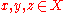 where
where  and
and  ,
,it is the case that
 for any
for any  .
.That is, the preference ordering P is convex if for any two goods bundles that are each viewed as being at least as good as a third bundle, a weighted average of the two bundles is also viewed as being at least as good as the third bundle.
Moreover,
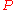 is strictly convex if for any
is strictly convex if for any where
where  ,
,  , and
, and  ,
,it is also true that
 for any
for any 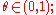
here
 can be translated as 'is better than' (in preference satisfaction). Thus the preference ordering P is strictly convex if for any two distinct goods bundles that are each viewed as being at least as good as a third bundle, a weighted average of the two bundles (including a positive amount of each bundle) is viewed as being better than the third bundle.
can be translated as 'is better than' (in preference satisfaction). Thus the preference ordering P is strictly convex if for any two distinct goods bundles that are each viewed as being at least as good as a third bundle, a weighted average of the two bundles (including a positive amount of each bundle) is viewed as being better than the third bundle.A set of convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
-shaped indifference curve
Indifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
s displays convex preferences: Given a convex indifference curve containing the set of all bundles (of two or more goods) that are all viewed as equally desired, the set of all goods bundles that are viewed as being at least as desired as those on the indifference curve is a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
.
Convex preferences with their associated convex indifference mapping arise from quasi-concave utility functions, although these are not necessary for the analysis of preferences.
See also
- Convex functionConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
- Level setLevel setIn mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
- Quasi-convex function
- Semi-continuous function
- Shapley–Folkman lemmaShapley–Folkman lemmaIn geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
- Wold, Herman O.Herman WoldHerman Ole Andreas Wold was a Norwegian-born econometrician and statistician who had a long career in Sweden...

