
Convex hull algorithms
Encyclopedia
Algorithms that construct convex hull
s of various objects have a broad range of applications in mathematics
and computer science
, see "Convex hull applications".
In computational geometry
, numerous algorithms are proposed for computing the convex hull of a finite set of points, with various computational complexities
.
Computing the convex hull means that a non-ambiguous and efficient representation
of the required convex shape is constructed. The complexity of the corresponding algorithms is usually estimated in terms of n, the number of input points, and h, the number of points on the convex hull.
If not all points are on the same line, then their convex hull is a convex polygon
whose vertices are some of the points in the input set. Its most common representation is the list of its vertices ordered along its boundary clockwise or counterclockwise. In some applications it is convenient to represent a convex polygon as an intersection of a set of half-planes
.
using the following reduction
. For the set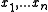 numbers to sort consider the set of points
numbers to sort consider the set of points 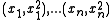 of points in the plane. Since they lie on a parabola
of points in the plane. Since they lie on a parabola
, which is a monotone curve it is easy to see that the vertices of the convex hull, when traversed along the boundary, produce the sorted order of the numbers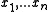 . Clearly, linear time is required for the described transformation of numbers into points and then extracting their sorted order. Therefore in the general case the convex hull of n points cannot be computed more quickly than sorting.
. Clearly, linear time is required for the described transformation of numbers into points and then extracting their sorted order. Therefore in the general case the convex hull of n points cannot be computed more quickly than sorting.
The standard Ω(n log n) lower bound for sorting is proven in the decision tree
model of computing, in which only numerical comparisons but not arithmetic operations can be performed; however, in this model, convex hulls cannot be computed at all. Sorting also requires Ω(n log n) time in the algebraic decision tree model of computation, a model that is more suitable for convex hulls, and in this model convex hulls also require Ω(n log n) time. However, in models of computer arithmetic that allow numbers to be sorted more quickly than O(n log n) time, for instance by using integer sorting
algorithms, planar convex hulls can also be computed more quickly: the Graham scan
algorithm for convex hulls consists of a single sorting step followed by a linear amount of additional work.
s. They may be asymptotically more efficient than Θ(n log n) algorithms in cases when h = o(n).
The lower bound on worst-case running time of output-sensitive convex hull algorithms was established to be Ω(n log h) in the planar case. There are several algorithms which attain this optimal time complexity
. The earliest one was introduced by Kirkpatrick
and Seidel
in 1986 (who called it "the ultimate convex hull algorithm"). A much simpler algorithm was developed by Chan
in 1996, and is called Chan's algorithm
.
and G. T. Toussaint, 1978. The idea is to quickly exclude many points that would not be part of the convex hull anyway. This method is based on the following idea. Find the two points with the lowest and highest x-coordinates, and the two points with the lowest and highest y-coordinates. (Each of these operations takes O
(n).) These four points form a convex quadrilateral
, and all points that lie in this quadrilateral (except for the four initially chosen vertices) are not part of the convex hull. Finding all of these points that lie in this quadrilateral is also O(n), and thus, the entire operation is O(n). Optionally, the points with smallest and largest sums of x- and y-coordinates as well as those with smallest and largest differences of x- and y-coordinates can also be added to the quadrilateral, thus forming an irregular convex octagon, whose insides can be safely discarded. If the points are random variables, then for a wide class of probability density functions, this throw-away pre-processing step will make a convex hull algorithm run in linear expected time, even if the worst-case complexity of the convex hull algorithm is quadratic in n.
Insertion of a point may increase the number of vertices of a convex hull at most by 1, while deletion may convert a 3-vertex convex hull into an n-1-vertex one.
The online version may be handled with O(log n) per point, which is asymptotically optimal. The dynamic version may be handled with O(log2 n) per operation.
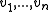 in O(n) time. The basic idea is very simple. The leftmost vertex is on the convex hull and we denote it
in O(n) time. The basic idea is very simple. The leftmost vertex is on the convex hull and we denote it 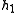 . The second point is assumed to be a candidate convex hull vertex as well. At each step one looks at three consecutive vertices of the polygon, with two first ones tentatively assigned to the growing convex hull and the third one is a new unprocessed vertex of the polygon, say, we denote this as
. The second point is assumed to be a candidate convex hull vertex as well. At each step one looks at three consecutive vertices of the polygon, with two first ones tentatively assigned to the growing convex hull and the third one is a new unprocessed vertex of the polygon, say, we denote this as 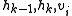 . If the angle is convex, then
. If the angle is convex, then 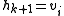 and the whole triple is shifted by one vertex along the polygon. If the resulting angle is concave, then the middle point (
and the whole triple is shifted by one vertex along the polygon. If the resulting angle is concave, then the middle point ( ) is deleted and the test is repeated for the triple
) is deleted and the test is repeated for the triple 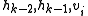 , etc. until we backtrack either to a convex angle or to point
, etc. until we backtrack either to a convex angle or to point 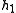 . After that the next (along the polygon) vertex is added to the triple to be tested, and the process repeats. However several previously published articles overlooked a possibility that deletion of a vertex from a polygon may result in a self-intersecting polygon, rendering further flow of the algorithm invalid. Fortunately, this case may also be handled efficiently. Later Tor and Middleditch (1984, "Convex Decomposition of Simple Polygons") and independently Melkman (1985, "Online Construction of the convex hull of a simple polyline") suggested a simpler approach with the same time complexity.
. After that the next (along the polygon) vertex is added to the triple to be tested, and the process repeats. However several previously published articles overlooked a possibility that deletion of a vertex from a polygon may result in a self-intersecting polygon, rendering further flow of the algorithm invalid. Fortunately, this case may also be handled efficiently. Later Tor and Middleditch (1984, "Convex Decomposition of Simple Polygons") and independently Melkman (1985, "Online Construction of the convex hull of a simple polyline") suggested a simpler approach with the same time complexity.
See also David Mount
's Lecture Notes for comparison. Refer to Lecture 4 for the latest developments, including
Chan's algorithm
.
For a finite set of points, the convex hull is a convex polyhedron in three dimensions, or in general a convex polytope
for any number of dimensions, whose vertices are some of the points in the input set. Its representation is not so simple as in the planar case, however. In higher dimensions, even if the vertices of a convex polytope are known, construction of its face
s is a non-trivial task, as is the dual problem of constructing the vertices given the faces. The size of the output may be exponentially larger than the size of the input, and even in cases where the input and output are both of comparable size the known algorithms for high-dimensional convex hulls are not output-sensitive
due both to issues with degenerate inputs and with intermediate results of high complexity.
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
s of various objects have a broad range of applications in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, see "Convex hull applications".
In computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, numerous algorithms are proposed for computing the convex hull of a finite set of points, with various computational complexities
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
.
Computing the convex hull means that a non-ambiguous and efficient representation
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
of the required convex shape is constructed. The complexity of the corresponding algorithms is usually estimated in terms of n, the number of input points, and h, the number of points on the convex hull.
Planar case
Consider the general case when the input to the algorithm is a finite unordered set of points on a Cartesian plane. An important special case in which the points are given in the order of traversal of a simple polygon's boundary is described later in a separate subsection.If not all points are on the same line, then their convex hull is a convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
whose vertices are some of the points in the input set. Its most common representation is the list of its vertices ordered along its boundary clockwise or counterclockwise. In some applications it is convenient to represent a convex polygon as an intersection of a set of half-planes
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
.
Lower bound on computational complexity
For a finite set of points in the plane the lower bound on the computational complexity of finding the convex hull represented as a convex polygon is easily shown to be the same as for sortingSorting
Sorting is any process of arranging items in some sequence and/or in different sets, and accordingly, it has two common, yet distinct meanings:# ordering: arranging items of the same kind, class, nature, etc...
using the following reduction
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
. For the set
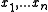 numbers to sort consider the set of points
numbers to sort consider the set of points 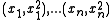 of points in the plane. Since they lie on a parabola
of points in the plane. Since they lie on a parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, which is a monotone curve it is easy to see that the vertices of the convex hull, when traversed along the boundary, produce the sorted order of the numbers
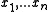 . Clearly, linear time is required for the described transformation of numbers into points and then extracting their sorted order. Therefore in the general case the convex hull of n points cannot be computed more quickly than sorting.
. Clearly, linear time is required for the described transformation of numbers into points and then extracting their sorted order. Therefore in the general case the convex hull of n points cannot be computed more quickly than sorting.The standard Ω(n log n) lower bound for sorting is proven in the decision tree
Decision tree
A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm. Decision trees are commonly used in operations research, specifically...
model of computing, in which only numerical comparisons but not arithmetic operations can be performed; however, in this model, convex hulls cannot be computed at all. Sorting also requires Ω(n log n) time in the algebraic decision tree model of computation, a model that is more suitable for convex hulls, and in this model convex hulls also require Ω(n log n) time. However, in models of computer arithmetic that allow numbers to be sorted more quickly than O(n log n) time, for instance by using integer sorting
Integer sorting
In computer science, integer sorting is the algorithmic problem of sorting a collection of data values by numeric keys, each of which is an integer. Algorithms designed for integer sorting may also often be applied to sorting problems in which the keys are floating point numbers or text strings...
algorithms, planar convex hulls can also be computed more quickly: the Graham scan
Graham scan
The Graham scan is a method of computing the convex hull of a finite set of points in the plane with time complexity O. It is named after Ronald Graham, who published the original algorithm in 1972...
algorithm for convex hulls consists of a single sorting step followed by a linear amount of additional work.
Optimal output-sensitive algorithms
As stated above, the complexity of finding a convex hull as a function the input size n is lower bounded by Ω(n log n). However, the complexity of some convex hull algorithms can be characterized in terms of both input size n and the output size h (the number of points in the hull). Such algorithms are called output-sensitive algorithmOutput-sensitive algorithm
In computer science, an output-sensitive algorithm is an algorithm whose running time depends not only on the size of the input but also on the size of the output...
s. They may be asymptotically more efficient than Θ(n log n) algorithms in cases when h = o(n).
The lower bound on worst-case running time of output-sensitive convex hull algorithms was established to be Ω(n log h) in the planar case. There are several algorithms which attain this optimal time complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
. The earliest one was introduced by Kirkpatrick
David G. Kirkpatrick
David Galer Kirkpatrick is a professor of computer science at the University of British Columbia. He is known for the Kirkpatrick–Seidel algorithm and his work on Polygon triangulation, and for co-inventing α-shapes and the β-skeleton...
and Seidel
Raimund Seidel
Raimund G. Seidel is a professor of computer scientist at the Universität des Saarlandes and an expert in computational geometry.Seidel was born in Graz, Austria, and studied with Hermann Maurer at the Graz University of Technology. He received his Ph.D. in 1987 from Cornell University under the...
in 1986 (who called it "the ultimate convex hull algorithm"). A much simpler algorithm was developed by Chan
Timothy M. Chan
Timothy Moon-Yew Chan is Professor and University Research Chairin the David R. Cheriton School of Computer Science, University of Waterloo, Canada.He graduated with BA from Rice University in 1992, and completed his Ph.D...
in 1996, and is called Chan's algorithm
Chan's algorithm
In computational geometry, Chan's algorithm, named after Timothy M. Chan, is an optimal output-sensitive algorithm to compute the convex hull of a set P of n points, in 2 or 3 dimensional space. The algorithm takes O time, where h is the number of vertices of the output...
.
Algorithms
Known convex hull algorithms are listed below, ordered by the date of first publication. Time complexity of each algorithm is stated in terms of the number of inputs points n and the number of points on the hull h. Note that in the worst case h may be as large as n.- Gift wrappingGift wrapping algorithmIn computational geometry, the gift wrapping algorithm is an algorithm for computing the convex hull of a given set of points.-Planar case:In the two-dimensional case the algorithm is also known as Jarvis march, after R. A. Jarvis, who published it in 1973; it has O time complexity, where n is the...
aka Jarvis march — O(nh)
One of the simplest (although not the most time efficient in the worst case) planar algorithms. Discovered independently by Chand & Kapur in 1970 and R. A. Jarvis in 1973. It has OBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(nh) time complexityComputational ComplexityComputational Complexity may refer to:*Computational complexity theory*Computational Complexity...
, where n is the number of points in the set, and h is the number of points in the hull. In the worst case the complexity is ΘBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n2).
- Graham scanGraham scanThe Graham scan is a method of computing the convex hull of a finite set of points in the plane with time complexity O. It is named after Ronald Graham, who published the original algorithm in 1972...
— O(n log n)
A slightly more sophisticated, but much more efficient algorithm, published by Ronald GrahamRonald GrahamRonald Lewis Graham is a mathematician credited by the American Mathematical Society as being "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years"...
in 1972. If the points are already sorted by one of the coordinates or by the angle to a fixed vector, then the algorithm takes O(n) time.
- QuickHull
Discovered independently in 1977 by W. Eddy and in 1978 by A. Bykat. Just like the quicksort algorithm, it has the expected time complexity of O(n log n), but may degenerate to Θ(nh) = O(n2) in the worst case.
- Divide and conquer — O(n log n)
Another O(n log n) algorithm, published in 1977 by PreparataFranco P. PreparataFranco P. Preparata is a computer scientist, the An Wang Professor of Computer Science at Brown University. He is best known for his 1985 computational geometry book with Michael Shamos, for many years the standard textbook in the field, but Preparata has worked in many other areas of computer...
and Hong. This algorithm is also applicable to the three dimensional case.
- Monotone chain — O(n log n)
Published in 1979 by A. M. Andrew. The algorithm can be seen as a variant of Graham scan which sorts the points lexicographically by their coordinates. When the input is already sorted, the algorithm takes O(n) time.
- Incremental convex hull algorithm — O(n log n)
Published in 1984 by Michael Kallay.
- Marriage-before-conquestKirkpatrick–Seidel algorithmThe Kirkpatrick–Seidel algorithm, called by its authors "the ultimate planar convex hull algorithm" is an algorithm for computing the convex hull of a set of points in the plane, with O time complexity, where n is the number of input points and h is the number of points in the hull...
— O(n log h)
The first optimal output-sensitive algorithm. Published by KirkpatrickDavid G. KirkpatrickDavid Galer Kirkpatrick is a professor of computer science at the University of British Columbia. He is known for the Kirkpatrick–Seidel algorithm and his work on Polygon triangulation, and for co-inventing α-shapes and the β-skeleton...
and SeidelRaimund SeidelRaimund G. Seidel is a professor of computer scientist at the Universität des Saarlandes and an expert in computational geometry.Seidel was born in Graz, Austria, and studied with Hermann Maurer at the Graz University of Technology. He received his Ph.D. in 1987 from Cornell University under the...
in 1986.
- Chan's algorithmChan's algorithmIn computational geometry, Chan's algorithm, named after Timothy M. Chan, is an optimal output-sensitive algorithm to compute the convex hull of a set P of n points, in 2 or 3 dimensional space. The algorithm takes O time, where h is the number of vertices of the output...
— O(n log h)
A simpler optimal output-sensitive algorithm discovered by ChanTimothy M. ChanTimothy Moon-Yew Chan is Professor and University Research Chairin the David R. Cheriton School of Computer Science, University of Waterloo, Canada.He graduated with BA from Rice University in 1992, and completed his Ph.D...
in 1996.
Akl-Toussaint heuristic
The following simple heuristic is often used as the first step in implementations of convex hull algorithms to improve their performance. It is based on the efficient convex hull algorithm by Selim AklSelim Akl
Selim G. Akl is a professor at Queen's University in the Queen's School of Computing, where he leads the . His research interests are primarily in the area of algorithm design and analysis, in particular for problems in parallel computing and unconventional computing. He is married, and has three...
and G. T. Toussaint, 1978. The idea is to quickly exclude many points that would not be part of the convex hull anyway. This method is based on the following idea. Find the two points with the lowest and highest x-coordinates, and the two points with the lowest and highest y-coordinates. (Each of these operations takes O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n).) These four points form a convex quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
, and all points that lie in this quadrilateral (except for the four initially chosen vertices) are not part of the convex hull. Finding all of these points that lie in this quadrilateral is also O(n), and thus, the entire operation is O(n). Optionally, the points with smallest and largest sums of x- and y-coordinates as well as those with smallest and largest differences of x- and y-coordinates can also be added to the quadrilateral, thus forming an irregular convex octagon, whose insides can be safely discarded. If the points are random variables, then for a wide class of probability density functions, this throw-away pre-processing step will make a convex hull algorithm run in linear expected time, even if the worst-case complexity of the convex hull algorithm is quadratic in n.
On-line and dynamic convex hull problems
The discussion above considers the case when all input points are known in advance. One may consider two other settings.- Online convex hull problem: Input points are obtained sequentially one by one. After each point arrives on input, the convex hull for the pointset obtained so far must be efficiently computed.
- Dynamic convex hull maintenance: The input points may be sequentially inserted or deleted, and the convex hull must be updated after each insert/delete operation.
Insertion of a point may increase the number of vertices of a convex hull at most by 1, while deletion may convert a 3-vertex convex hull into an n-1-vertex one.
The online version may be handled with O(log n) per point, which is asymptotically optimal. The dynamic version may be handled with O(log2 n) per operation.
Simple polygon
McCallum and Avis were first to provide a correct algorithm to construct the convex hull of a simple polygonSimple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
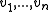 in O(n) time. The basic idea is very simple. The leftmost vertex is on the convex hull and we denote it
in O(n) time. The basic idea is very simple. The leftmost vertex is on the convex hull and we denote it 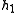 . The second point is assumed to be a candidate convex hull vertex as well. At each step one looks at three consecutive vertices of the polygon, with two first ones tentatively assigned to the growing convex hull and the third one is a new unprocessed vertex of the polygon, say, we denote this as
. The second point is assumed to be a candidate convex hull vertex as well. At each step one looks at three consecutive vertices of the polygon, with two first ones tentatively assigned to the growing convex hull and the third one is a new unprocessed vertex of the polygon, say, we denote this as 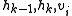 . If the angle is convex, then
. If the angle is convex, then 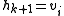 and the whole triple is shifted by one vertex along the polygon. If the resulting angle is concave, then the middle point (
and the whole triple is shifted by one vertex along the polygon. If the resulting angle is concave, then the middle point ( ) is deleted and the test is repeated for the triple
) is deleted and the test is repeated for the triple 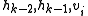 , etc. until we backtrack either to a convex angle or to point
, etc. until we backtrack either to a convex angle or to point 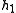 . After that the next (along the polygon) vertex is added to the triple to be tested, and the process repeats. However several previously published articles overlooked a possibility that deletion of a vertex from a polygon may result in a self-intersecting polygon, rendering further flow of the algorithm invalid. Fortunately, this case may also be handled efficiently. Later Tor and Middleditch (1984, "Convex Decomposition of Simple Polygons") and independently Melkman (1985, "Online Construction of the convex hull of a simple polyline") suggested a simpler approach with the same time complexity.
. After that the next (along the polygon) vertex is added to the triple to be tested, and the process repeats. However several previously published articles overlooked a possibility that deletion of a vertex from a polygon may result in a self-intersecting polygon, rendering further flow of the algorithm invalid. Fortunately, this case may also be handled efficiently. Later Tor and Middleditch (1984, "Convex Decomposition of Simple Polygons") and independently Melkman (1985, "Online Construction of the convex hull of a simple polyline") suggested a simpler approach with the same time complexity.Higher dimensions
A number of algorithms are known for the three-dimensional case, as well as for arbitrary dimensions. See http://www.cse.unsw.edu.au/~lambert/java/3d/hull.html.See also David Mount
David Mount
David Mount is currently a Professor at The University of Maryland whose research is in Computational Geometry.-Biography:David Mount received a B.S. in Computer Science at Purdue University in 1977 and received his Ph.D...
's Lecture Notes for comparison. Refer to Lecture 4 for the latest developments, including
Chan's algorithm
Chan's algorithm
In computational geometry, Chan's algorithm, named after Timothy M. Chan, is an optimal output-sensitive algorithm to compute the convex hull of a set P of n points, in 2 or 3 dimensional space. The algorithm takes O time, where h is the number of vertices of the output...
.
For a finite set of points, the convex hull is a convex polyhedron in three dimensions, or in general a convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
for any number of dimensions, whose vertices are some of the points in the input set. Its representation is not so simple as in the planar case, however. In higher dimensions, even if the vertices of a convex polytope are known, construction of its face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
s is a non-trivial task, as is the dual problem of constructing the vertices given the faces. The size of the output may be exponentially larger than the size of the input, and even in cases where the input and output are both of comparable size the known algorithms for high-dimensional convex hulls are not output-sensitive
Output-sensitive algorithm
In computer science, an output-sensitive algorithm is an algorithm whose running time depends not only on the size of the input but also on the size of the output...
due both to issues with degenerate inputs and with intermediate results of high complexity.
Further reading
- Thomas H. CormenThomas H. CormenThomas H. Cormen is the co-author of Introduction to Algorithms, along with Charles Leiserson, Ron Rivest, and Cliff Stein. He is a Full Professor of computer science at Dartmouth College and currently Chair of the Dartmouth College Department of Computer Science. Between 2004 and 2008 he directed...
, Charles E. LeisersonCharles E. LeisersonCharles Eric Leiserson is a computer scientist, specializing in the theory of parallel computing and distributed computing, and particularly practical applications thereof; as part of this effort, he developed the Cilk multithreaded language...
, Ronald L. Rivest, and Clifford SteinClifford SteinClifford Stein, a computer scientist, is currently a professor of industrial engineering and operations research at Columbia University in New York, NY, where he also holds an appointment in the Department of Computer Science. Stein is chair of the Industrial Engineering and Operations Research...
. Introduction to AlgorithmsIntroduction to AlgorithmsIntroduction to Algorithms is a book by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. It is used as the textbook for algorithms courses at many universities. It is also one of the most commonly cited references for algorithms in published papers, with over 4600...
, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 33.3: Finding the convex hull, pp. 947–957. - Franco P. PreparataFranco P. PreparataFranco P. Preparata is a computer scientist, the An Wang Professor of Computer Science at Brown University. He is best known for his 1985 computational geometry book with Michael Shamos, for many years the standard textbook in the field, but Preparata has worked in many other areas of computer...
, S.J. Hong. Convex Hulls of Finite Sets of Points in Two and Three Dimensions, Commun. ACM, vol. 20, no. 2, pp. 87–93, 1977. Section 1.1: An Example: Convex Hulls (describes classical algorithms for 2-dimensional convex hulls). Chapter 11: Convex Hulls: pp. 235–250 (describes a randomized algorithm for 3-dimensional convex hulls due to Clarkson and Shor).
External links
- 2D, 3D, and dD Convex Hull in CGALCGALThe Computational Geometry Algorithms Library is a software library that aims to provide easy access to efficient and reliable algorithms in computational geometry. While primarily written in C++, Python and Scilab bindings are also available....
, the Computational Geometry Algorithms Library - Qhull code for Convex Hull, Delaunay Triangulation, Voronoi Diagram, and Halfspace Intersection
- Demo as Flash swf, Jarvis, Graham, Quick (divide and conquer) and Chan algorithms

