Consistent pricing process
Encyclopedia
A consistent pricing process (CPP) is any representation of (frictionless
) "prices" of assets in a market. It is a stochastic process
in a filtered probability space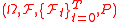
such that at time 
the 
component can be thought of as a price for the 
asset.
Mathematically, a CPP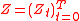
in a market with d-assets is an adapted process
in
if Z is a martingale
with respect to the physical probability measure
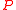, and if 
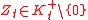at all times 
such that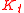 
is the solvency cone
for the market at time
.
The CPP plays the role of an equivalent martingale measure in markets with transaction costs. In particular, there exists a 1-to-1 correspondence between the CPP
and the EMM 
.
Frictionless market
A Frictionless market is a financial market without transaction costs. Friction is a type of market incompleteness. Every complete market is frictionless, but the converse does not hold. In a frictionless market the solvency cone is the halfspace normal to the unique price vector. The...
) "prices" of assets in a market. It is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
in a filtered probability space
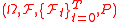such that at time the component can be thought of as a price for the asset.Mathematically, a CPP
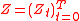in a market with d-assets is an adapted processAdapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
in
if Z is a martingaleMartingale
Martingale can refer to:*Martingale , a stochastic process in which the conditional expectation of the next value, given the current and preceding values, is the current value*Martingale for horses...
with respect to the physical probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
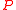, and if 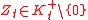at all times such that 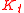is the solvency coneSolvency cone
The solvency cone is a concept used in financial mathematics which models the possible trades in the financial market. This is of particular interest to markets with transaction costs...
for the market at time
.The CPP plays the role of an equivalent martingale measure in markets with transaction costs. In particular, there exists a 1-to-1 correspondence between the CPP
and the EMM .