Consistent heuristic
Encyclopedia
In computer science
, a consistent (or monotone) heuristic function
is a strategy for search
that approaches the solution in an incremental way without taking any step back. Formally, for every node N and every successor P of N generated by any action a, the estimated cost of reaching the goal from N is no greater than the step cost of getting to P plus the estimated cost of reaching the goal from P. In other words:
where
A consistent heuristic is also admissible
. This is proved by induction on
, the length of the best path from node to goal. By assumption, 
, where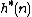 
denotes the cost of the shortest path from n to the goal. Therefore,
,
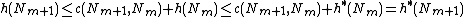making it admissible. (
is any node whose best path to the goal, of length m+1, goes through some immediate child 
whose best path to the goal is of length m.)
Note: not all admissible heuristics are consistent.
However, an admissible heuristic
, can be made into a consistent heuristic,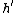 
, through the following adjustment:
(Known as the pathmax equation.)
is monotonically non-decreasing along the best path to the goal, where 
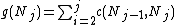is the cost of the best path from start node 
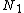to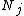 
. It's necessary and sufficient for a heuristic to obey the triangle inequality
in order to be consistent.
In the A* search algorithm, using a consistent heuristic means that once a node is expanded, the cost by which it was reached is the lowest possible, under the same conditions that Dijkstra's algorithm requires in solving the shortest path problem
(no negative cost cycles). In fact, if the search graph is given cost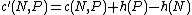
for a consistent 
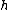, then A* is equivalent to best-first search on that graph using Dijkstra's algorithm. In the unusual event that an admissible heuristic is not consistent, a node will need repeated expansion every time a new best (so-far) cost is achieved for it.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a consistent (or monotone) heuristic function
Heuristic function
A heuristic function, or simply a heuristic, is a function that ranks alternatives in various search algorithms at each branching step based on the available information in order to make a decision about which branch to follow during a search.-Shortest paths:For example, for shortest path...
is a strategy for search
Search algorithm
In computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
that approaches the solution in an incremental way without taking any step back. Formally, for every node N and every successor P of N generated by any action a, the estimated cost of reaching the goal from N is no greater than the step cost of getting to P plus the estimated cost of reaching the goal from P. In other words:
-
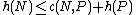and -
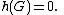
where
- h is the consistent heuristic function
- N is any node in the graph
- P is any child of N
- G is any goal node.
A consistent heuristic is also admissible
Admissible heuristic
In computer science, specifically in algorithms related to Pathfinding, a heuristic function is said to be admissible if it is no more than the lowest-cost path to the goal. In other words, a heuristic is admissible if it never overestimates the cost of reaching the goal...
. This is proved by induction on
, the length of the best path from node to goal. By assumption, , where 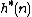denotes the cost of the shortest path from n to the goal. Therefore,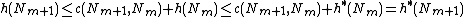,making it admissible. (
is any node whose best path to the goal, of length m+1, goes through some immediate child whose best path to the goal is of length m.)Note: not all admissible heuristics are consistent.
However, an admissible heuristic
, can be made into a consistent heuristic, 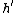, through the following adjustment:
(Known as the pathmax equation.)
Consequences of monotonicity
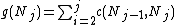Consistent heuristics are called monotone because the estimated final cost of a partial solution, is monotonically non-decreasing along the best path to the goal, where is the cost of the best path from start node 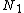to 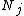. It's necessary and sufficient for a heuristic to obey the triangle inequalityTriangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
in order to be consistent.
In the A* search algorithm, using a consistent heuristic means that once a node is expanded, the cost by which it was reached is the lowest possible, under the same conditions that Dijkstra's algorithm requires in solving the shortest path problem
Shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
(no negative cost cycles). In fact, if the search graph is given cost
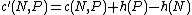for a consistent , then A* is equivalent to best-first search on that graph using Dijkstra's algorithm. In the unusual event that an admissible heuristic is not consistent, a node will need repeated expansion every time a new best (so-far) cost is achieved for it.External links
- CS141 Lecture from Brown University http://cs.brown.edu/courses/csci1410/amy_notes/graphs.pdf