Conditionality principle
Encyclopedia
The conditionality principle is a Fisherian principle of statistical inference
that Allan Birnbaum
formally defined and studied in his 1962 JASA
article. Together with the sufficiency principle, Birnbaum's version of the principle implies the famous likelihood principle
. Although the relevance of the proof to data analysis remains controversial among statisticians, many Bayesians and likelihoodists consider the likelihood principle foundational for statistical inference.
(i.e. a statistic whose probability distribution does not depend on unknown parameter values). This means that observing a specific outcome x of experiment E is equivalent to observing the value of h and taking an observation xh from the component experiment Eh.
The conditionality principle can be formally stated thus:
Conditionality Principle: If E is any experiment having the form of a mixture of component experiments Eh, then for each outcome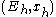
of E, [...] the evidential meaning of any outcome x of any mixture experiment E is the same as that of the corresponding outcome xh of the corresponding component experiment Eh, ignoring the over-all structure of the mixed experiment. (See Birnbaum 1962)
Informally, the conditionality principle can be taken as to claim the irrelevance of component experiments that were not actually performed.
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
that Allan Birnbaum
Allan Birnbaum
Allan Birnbaum was an American statistician who contributed to statistical inference, foundations of statistics, statistical genetics, statistical psychology, and history of statistics....
formally defined and studied in his 1962 JASA
JASA
JASA, as an initialism, stands for:*Japan-America Security Alliance, signed in 1951*Journal of the Acoustical Society of America*Journal of the American Statistical Association*The JASA Brand of Disposable food packaging products in Malaysia...
article. Together with the sufficiency principle, Birnbaum's version of the principle implies the famous likelihood principle
Likelihood principle
In statistics,the likelihood principle is a controversial principle of statistical inference which asserts that all of the information in a sample is contained in the likelihood function....
. Although the relevance of the proof to data analysis remains controversial among statisticians, many Bayesians and likelihoodists consider the likelihood principle foundational for statistical inference.
Formulation
The conditionality principle makes an assertion about an experiment E that can be described as a mixture of several component experiments Eh where h is an ancillary statisticAncillary statistic
In statistics, an ancillary statistic is a statistic whose sampling distribution does not depend on which of the probability distributions among those being considered is the distribution of the statistical population from which the data were taken...
(i.e. a statistic whose probability distribution does not depend on unknown parameter values). This means that observing a specific outcome x of experiment E is equivalent to observing the value of h and taking an observation xh from the component experiment Eh.
The conditionality principle can be formally stated thus:
Conditionality Principle: If E is any experiment having the form of a mixture of component experiments Eh, then for each outcome
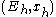of E, [...] the evidential meaning of any outcome x of any mixture experiment E is the same as that of the corresponding outcome xh of the corresponding component experiment Eh, ignoring the over-all structure of the mixed experiment. (See Birnbaum 1962)Informally, the conditionality principle can be taken as to claim the irrelevance of component experiments that were not actually performed.