
Coherence (philosophical gambling strategy)
Encyclopedia
In a thought experiment
proposed by the Italian probabilist Bruno de Finetti
in order to justify Bayesian probability
, an array of wagers is coherent precisely if it does not expose the wagerer to certain loss regardless of the outcomes of events on which he is wagering, even if his opponent makes the most judicious choices.
.
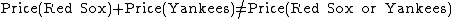
But if you set the price of the third ticket too low, your prudent opponent will buy that ticket and sell you the other two tickets. By considering the three possible outcomes (Red Sox, Yankees, some other team), you will see that regardless of which of the three outcomes eventuates, you lose. An analogous fate awaits you if you set the price of the third ticket too high relative to the other two prices. This parallels the fact that probabilities of mutually exclusive events are additive (see probability axioms
).
Three outcomes are possible: The game is cancelled; the game is played and the Red Sox lose; the game is played and the Red Sox win. You may set the prices in such a way that

(where the second price above is that of the bet that includes the refund in case of cancellation). (Note: The prices here are the dimensionless numbers obtained by dividing by $1, which is the payout in all three cases.) Your prudent opponent writes three linear inequalities in three variables. The variables are the amounts he will invest in each of the three promises; the value of one of these is negative if he will make you buy that promise and positive if he will buy it from you. Each inequality corresponds to one of the three possible outcomes. Each inequality states that your opponent's net gain is more than zero. A solution exists if and only if the determinant
of the matrix is not zero. That determinant is:
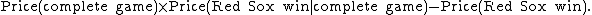
Thus your prudent opponent can make you a sure loser unless you set your prices in a way that parallels the simplest conventional characterization of conditional probability
.
and related results such as the inclusion-exclusion principle
(but not necessarily countable additivity).
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
proposed by the Italian probabilist Bruno de Finetti
Bruno de Finetti
Bruno de Finetti was an Italian probabilist, statistician and actuary, noted for the "operational subjective" conception of probability...
in order to justify Bayesian probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
, an array of wagers is coherent precisely if it does not expose the wagerer to certain loss regardless of the outcomes of events on which he is wagering, even if his opponent makes the most judicious choices.
Operational subjective probabilities as wagering odds
You must set the price of a promise to pay $1 if John Smith wins tomorrow's election, and $0 otherwise. You know that your opponent will be able to choose either to buy such a promise from you at the price you have set, or require you to buy such a promise from him/her, still at the same price. In other words: you set the odds, but your opponent decides which side of the bet will be yours. The price you set is the "operational subjective probability" that you assign to the proposition on which you are betting."Dutch books"
A person who has set prices on an array of wagers in such a way that he or she will make a net gain regardless of the outcome, is said to have made a Dutch bookDutch book
In gambling a Dutch book or lock is a set of odds and bets which guarantees a profit, regardless of the outcome of the gamble. It is associated with probabilities implied by the odds not being coherent....
.
A very trivial Dutch book
The rules do not forbid you to set a price higher than $1, but if you do, your prudent opponent may sell you that high-priced ticket, and then your opponent comes out ahead regardless of the outcome of the event on which you bet. Neither are you forbidden to set a negative price, but then your opponent may make you pay him to accept a promise from you to pay him later if a certain contingency eventuates. Either way, you lose. These lose-lose situations parallel the fact that a probability can neither exceed 1 nor be less than 0.A somewhat less trivial and more instructive Dutch book
Now suppose you set the price of a promise to pay $1 if the Boston Red Sox win next year's World Series, and also the price of a promise to pay $1 if the New York Yankees win, and finally the price of a promise to pay $1 if either the Red Sox or the Yankees win. You may set the prices in such a way that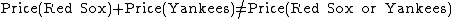
But if you set the price of the third ticket too low, your prudent opponent will buy that ticket and sell you the other two tickets. By considering the three possible outcomes (Red Sox, Yankees, some other team), you will see that regardless of which of the three outcomes eventuates, you lose. An analogous fate awaits you if you set the price of the third ticket too high relative to the other two prices. This parallels the fact that probabilities of mutually exclusive events are additive (see probability axioms
Probability axioms
In probability theory, the probability P of some event E, denoted P, is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov, which are described below....
).
Conditional wagers and conditional probabilities
Now imagine a more complicated scenario. You must set the prices of three promises:- to pay $1 if the Red Sox win tomorrow's game; the purchaser of this promise loses his bet if the Red Sox do not win regardless of whether their failure is due to their loss of a completed game or cancellation of the game, and
- to pay $1 if the Red Sox win, and to refund the price of the promise if the game is cancelled, and
- to pay $1 if the game is completed, regardless of who wins.
Three outcomes are possible: The game is cancelled; the game is played and the Red Sox lose; the game is played and the Red Sox win. You may set the prices in such a way that

(where the second price above is that of the bet that includes the refund in case of cancellation). (Note: The prices here are the dimensionless numbers obtained by dividing by $1, which is the payout in all three cases.) Your prudent opponent writes three linear inequalities in three variables. The variables are the amounts he will invest in each of the three promises; the value of one of these is negative if he will make you buy that promise and positive if he will buy it from you. Each inequality corresponds to one of the three possible outcomes. Each inequality states that your opponent's net gain is more than zero. A solution exists if and only if the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix is not zero. That determinant is:
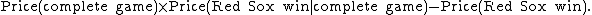
Thus your prudent opponent can make you a sure loser unless you set your prices in a way that parallels the simplest conventional characterization of conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
.
Coherence
It can be shown that the set of prices is coherent when they satisfy the probability axiomsProbability axioms
In probability theory, the probability P of some event E, denoted P, is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov, which are described below....
and related results such as the inclusion-exclusion principle
Inclusion-exclusion principle
In combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
(but not necessarily countable additivity).

