
Circuit (computer theory)
Encyclopedia
A circuit in computer theory is a theoretical structure simulating electrical and data paths, in which voltage and binary values enter at the beginning of the circuit, go through gates which do some computation and output an answer. An important special case of circuits is the boolean circuit
.
Circuits are defined in terms of the gates they contain and the values the gates can take. For example, binary circuits' values are boolean values, and the gates can be binary
AND and OR gates and unary
NOT gates. In integer circuit
s, the values are set of integers and the gates are set union, intersection, complement, and the arithmetic operations + and
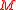 , a set of gate labels
, a set of gate labels 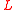 which are families of functions from
which are families of functions from 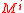 to
to 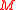 , where
, where  is a non-negative integer (with
is a non-negative integer (with  for constant gates), and a labelled directed acyclic graph
for constant gates), and a labelled directed acyclic graph
, the labels of which are elements of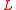 , a gate
, a gate 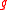 can label a node
can label a node  of in-degree
of in-degree  if and only if
if and only if 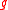 is defined on
is defined on 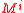 .
.
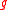 to
to 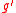 then
then 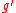 is called a child of
is called a child of 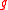 , we suppose there is an order on the vertices, so we can speak of the
, we suppose there is an order on the vertices, so we can speak of the  th child of a vertex when
th child of a vertex when  is less than the in-degree of this vertex.
is less than the in-degree of this vertex.
The size of a circuit is the number of nodes of a circuit.
The depth of a node is the size of the longest path beginning in
is the size of the longest path beginning in  , in particular, the gates of out-degree 0 are the only gates of depth 1. The depth of the circuit is the size of the longest path in the circuit. The level
, in particular, the gates of out-degree 0 are the only gates of depth 1. The depth of the circuit is the size of the longest path in the circuit. The level  is the set of gates of depth
is the set of gates of depth  .
.
A levelled circuit is a circuit where the edges to nodes of depth comes only from nodes of depth
comes only from nodes of depth  or from input nodes. Another way to see it is that there are edges only between adjacent levels.
or from input nodes. Another way to see it is that there are edges only between adjacent levels.
The width of a labelled circuit is the size of the biggest level.
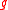 of in-degree
of in-degree  and label
and label 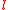 is
is  where
where 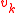 is the value of the
is the value of the  th son of
th son of 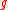 .
.
There is one node of out-degree 0 which will be called the output node, the value of the circuit is the value of the output node.
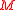 . If there are
. If there are  variables, then the circuit can be seen as a function from
variables, then the circuit can be seen as a function from 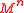 to
to 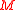 . It is then usual to consider a family of circuits
. It is then usual to consider a family of circuits 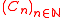 , a sequence of circuits indexed by the integers where the circuit
, a sequence of circuits indexed by the integers where the circuit 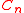 has
has  variables. Families of circuits can thus be seen as functions from
variables. Families of circuits can thus be seen as functions from 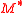 to
to 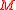 .
.
The notions of size, depth and width can be naturally extended to families of functions, they become functions from to
to  , for example size(
, for example size( ) is the size of the
) is the size of the  th circuit of the family.
th circuit of the family.
It is usual for some kind of circuits, like boolean circuit
, to add restrictions to the circuits one can accept in the family, like having a bounded width, that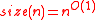 , which means that the size function of a given family is bounded by a polynomial, that
, which means that the size function of a given family is bounded by a polynomial, that 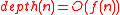 for any function
for any function 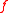 , that the in-degree should be bounded, either by a constant or by a polynomial in the number of inputs.
, that the in-degree should be bounded, either by a constant or by a polynomial in the number of inputs.
and algorithm
theory, there are two different questions one may want to answer:
Boolean circuit
A Boolean circuit is a mathematical model of computation used in studying computational complexity theory. Boolean circuits are the main object of study in circuit complexity and are a special kind of circuits; a formal language can be decided by a family of Boolean circuits, one circuit for each...
.
Circuits are defined in terms of the gates they contain and the values the gates can take. For example, binary circuits' values are boolean values, and the gates can be binary
Binary function
In mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
AND and OR gates and unary
Unary
* Unary numeral system, the simplest numeral system to represent natural numbers* Unary operation, a kind of mathematical operator that has only one operand* Unary coding, an entropy encoding that represents a number n with n − 1 ones followed by a zero...
NOT gates. In integer circuit
Integer circuit
Integer circuits is a mathematical model used in studying computational complexity theory. It is a special case of circuit, the object is a labeled directed acyclic graph the nodes of which evaluate to sets of integers, the leaves are finite sets, and the gates are set operations or arithmetic...
s, the values are set of integers and the gates are set union, intersection, complement, and the arithmetic operations + and

Formal definition
A circuit is composed of a set of values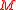 , a set of gate labels
, a set of gate labels 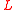 which are families of functions from
which are families of functions from 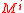 to
to 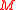 , where
, where  is a non-negative integer (with
is a non-negative integer (with  for constant gates), and a labelled directed acyclic graph
for constant gates), and a labelled directed acyclic graphDirected acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
, the labels of which are elements of
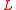 , a gate
, a gate 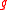 can label a node
can label a node  of in-degree
of in-degree  if and only if
if and only if 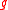 is defined on
is defined on 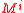 .
.Notions
The nodes of in-degree 0 are called the input nodes, or the leaves. If there is an edge from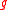 to
to 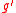 then
then 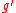 is called a child of
is called a child of 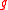 , we suppose there is an order on the vertices, so we can speak of the
, we suppose there is an order on the vertices, so we can speak of the  th child of a vertex when
th child of a vertex when  is less than the in-degree of this vertex.
is less than the in-degree of this vertex.The size of a circuit is the number of nodes of a circuit.
The depth of a node
 is the size of the longest path beginning in
is the size of the longest path beginning in  , in particular, the gates of out-degree 0 are the only gates of depth 1. The depth of the circuit is the size of the longest path in the circuit. The level
, in particular, the gates of out-degree 0 are the only gates of depth 1. The depth of the circuit is the size of the longest path in the circuit. The level  is the set of gates of depth
is the set of gates of depth  .
.A levelled circuit is a circuit where the edges to nodes of depth
 comes only from nodes of depth
comes only from nodes of depth  or from input nodes. Another way to see it is that there are edges only between adjacent levels.
or from input nodes. Another way to see it is that there are edges only between adjacent levels.The width of a labelled circuit is the size of the biggest level.
Evaluation
The value of a node is defined recursively on the depth of the nodes, the gate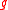 of in-degree
of in-degree  and label
and label 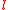 is
is  where
where 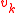 is the value of the
is the value of the  th son of
th son of 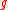 .
.There is one node of out-degree 0 which will be called the output node, the value of the circuit is the value of the output node.
Circuit as functions
The labels of the leaves can also be variables which take values in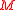 . If there are
. If there are  variables, then the circuit can be seen as a function from
variables, then the circuit can be seen as a function from 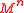 to
to 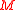 . It is then usual to consider a family of circuits
. It is then usual to consider a family of circuits 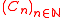 , a sequence of circuits indexed by the integers where the circuit
, a sequence of circuits indexed by the integers where the circuit 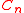 has
has  variables. Families of circuits can thus be seen as functions from
variables. Families of circuits can thus be seen as functions from 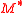 to
to 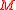 .
.The notions of size, depth and width can be naturally extended to families of functions, they become functions from
 to
to  , for example size(
, for example size( ) is the size of the
) is the size of the  th circuit of the family.
th circuit of the family.It is usual for some kind of circuits, like boolean circuit
Boolean circuit
A Boolean circuit is a mathematical model of computation used in studying computational complexity theory. Boolean circuits are the main object of study in circuit complexity and are a special kind of circuits; a formal language can be decided by a family of Boolean circuits, one circuit for each...
, to add restrictions to the circuits one can accept in the family, like having a bounded width, that
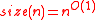 , which means that the size function of a given family is bounded by a polynomial, that
, which means that the size function of a given family is bounded by a polynomial, that 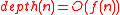 for any function
for any function 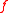 , that the in-degree should be bounded, either by a constant or by a polynomial in the number of inputs.
, that the in-degree should be bounded, either by a constant or by a polynomial in the number of inputs.Complexity and algorithmic problems
Circuit are often used in computational complexityComputational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
and algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
theory, there are two different questions one may want to answer:
- Given a circuit, what is the complexity of computing the value of its output. For example, over boolean circuitBoolean circuitA Boolean circuit is a mathematical model of computation used in studying computational complexity theory. Boolean circuits are the main object of study in circuit complexity and are a special kind of circuits; a formal language can be decided by a family of Boolean circuits, one circuit for each...
s, this question is P complete and over integer circuitInteger circuitInteger circuits is a mathematical model used in studying computational complexity theory. It is a special case of circuit, the object is a labeled directed acyclic graph the nodes of which evaluate to sets of integers, the leaves are finite sets, and the gates are set operations or arithmetic...
s it is not known to be decidable. - Given a language, what is the minimal size (resp. depth) function which recognizes the language. It is here that, usually, some restrictions are added to the form of the circuits. Over boolean circuitBoolean circuitA Boolean circuit is a mathematical model of computation used in studying computational complexity theory. Boolean circuits are the main object of study in circuit complexity and are a special kind of circuits; a formal language can be decided by a family of Boolean circuits, one circuit for each...
this creates formalism like NCNC (complexity)In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
.

