Chevalley scheme
Encyclopedia
A Chevalley scheme in algebraic geometry
was a precursor notion of scheme theory.
Let X be a separated integral noetherian scheme, R its function field
. If we denote by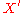
the set of subrings 
of R, where x runs through X (when 
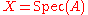, we denote 
by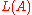 
), 
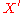verifies the following three properties
Originally, Chevalley also supposed that R was an extension of finite type of a field K and that the
's were algebras of finite type over a field too (this simplifies the second condition above).
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
was a precursor notion of scheme theory.
Let X be a separated integral noetherian scheme, R its function field
Function field
Function field may refer to:*Function field of an algebraic variety*Function field...
. If we denote by
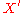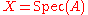the set of subrings of R, where x runs through X (when , we denote by 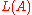), 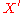verifies the following three properties
- For each
, R is the field of fractions of M. - There is a finite set of noetherian subrings
of R so that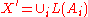 
and that, for each pair of indices i,j, the subring 
of R generated by 
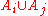is an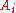 
-algebra of finite type. - If
in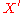 
are such that the maximal ideal of M is contained in that of N, then M=N.
Originally, Chevalley also supposed that R was an extension of finite type of a field K and that the
's were algebras of finite type over a field too (this simplifies the second condition above).