
Channel-state duality
Encyclopedia
In quantum information theory, the channel-state duality refers to the correspondence between quantum channel
s and quantum states (described by density matrices
). Phrased differently, the duality is the isomorphism between completely positive maps (channels) from A to Cn×n, where A is a C*-algebra and Cn×n denotes the n×n complex entries, and positive linear functionals (state
s) on the tensor product
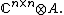
, in the Schrödinger picture, is a completely positive (CP for short) linear map
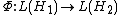
that takes a state of system 1 to a state of system 2. Next we describe the dual state corresponding to Φ.
Let Ei j denote the matrix unit whose ij-th entry is 1 and zero elsewhere. The (operator) matrix
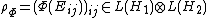
is called the Choi matrix of Φ. By Choi's theorem on completely positive maps
, Φ is CP if and only if ρΦ is positive (semidefinite). One can view ρΦ as a density matrix, and therefore the state dual to Φ.
The duality between channels and states refers to the map
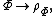
a linear bijection. This map is also called Jamiołkowski isomorphism or Choi–Jamiołkowski isomorphism.
Quantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
s and quantum states (described by density matrices
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
). Phrased differently, the duality is the isomorphism between completely positive maps (channels) from A to Cn×n, where A is a C*-algebra and Cn×n denotes the n×n complex entries, and positive linear functionals (state
State (functional analysis)
In functional analysis, a state on a C*-algebra is a positive linear functional of norm 1. The set of states of a C*-algebra A, sometimes denoted by S, is always a convex set. The extremal points of S are called pure states...
s) on the tensor product
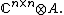
Details
Let H1 and H2 be (finite dimensional) Hilbert spaces. The family of linear operators acting on Hi will be denoted by L(Hi). Consider two quantum systems, indexed by 1 and 2, whose states are density matrices in L(Hi) respectively. A quantum channelQuantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
, in the Schrödinger picture, is a completely positive (CP for short) linear map
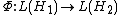
that takes a state of system 1 to a state of system 2. Next we describe the dual state corresponding to Φ.
Let Ei j denote the matrix unit whose ij-th entry is 1 and zero elsewhere. The (operator) matrix
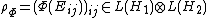
is called the Choi matrix of Φ. By Choi's theorem on completely positive maps
Choi's theorem on completely positive maps
In mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
, Φ is CP if and only if ρΦ is positive (semidefinite). One can view ρΦ as a density matrix, and therefore the state dual to Φ.
The duality between channels and states refers to the map
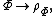
a linear bijection. This map is also called Jamiołkowski isomorphism or Choi–Jamiołkowski isomorphism.

