
Catalan's constant
Encyclopedia
In mathematics
, Catalan's constant G, which occasionally appears in estimates in combinatorics
, is defined by
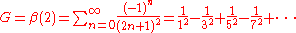
where β is the Dirichlet beta function
.
Its numerical value http://www.gutenberg.org/etext/812 is approximately
It is not known whether G is irrational
, let alone transcendental
.
Catalan's constant was named after Eugène Charles Catalan
.
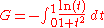
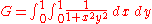

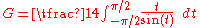

along with
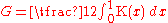
where K(x) is a complete elliptic integral
of the first kind, and
 .
.
, as well as in values of the second polygamma function, also called the trigamma function
, at fractional arguments:

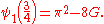
Simon Plouffe
gives an infinite collection of identities between the trigamma function, and Catalan's constant; these are expressible as paths on a graph.
and Catalan's constant; these are expressible as paths on a graph.
It also appears in connection with the hyperbolic secant distribution.
and
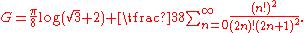
The theoretical foundations for such series is given by Broadhurst (the first formula) and Ramanujan (the second formula) The algorithms for fast evaluation of the Catalan constant is constructed by E. Karatsuba.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Catalan's constant G, which occasionally appears in estimates in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, is defined by
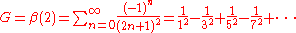
where β is the Dirichlet beta function
Dirichlet beta function
In mathematics, the Dirichlet beta function is a special function, closely related to the Riemann zeta function...
.
Its numerical value http://www.gutenberg.org/etext/812 is approximately
- G = 0.915 965 594 177 219 015 054 603 514 932 384 110 774 …
It is not known whether G is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, let alone transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
.
Catalan's constant was named after Eugène Charles Catalan
Eugène Charles Catalan
Eugène Charles Catalan was a French and Belgian mathematician.- Biography :Catalan was born in Bruges , the only child of a French jeweller by the name of Joseph Catalan, in 1814. In 1825, he traveled to Paris and learned mathematics at École Polytechnique, where he met Joseph Liouville...
.
Integral identities
Some identities include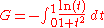
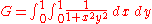

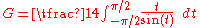

along with
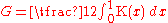
where K(x) is a complete elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
of the first kind, and
 .
.Uses
G appears in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, as well as in values of the second polygamma function, also called the trigamma function
Trigamma function
In mathematics, the trigamma function, denoted ψ1, is the second of the polygamma functions, and is defined byIt follows from this definition thatwhere ψ is the digamma function...
, at fractional arguments:

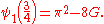
Simon Plouffe
Simon Plouffe
Simon Plouffe is a Quebec mathematician born on June 11, 1956 in Saint-Jovite, Quebec. He discovered the formula for the BBP algorithm which permits the computation of the nth binary digit of π, in 1995...
gives an infinite collection of identities between the trigamma function,
 and Catalan's constant; these are expressible as paths on a graph.
and Catalan's constant; these are expressible as paths on a graph.It also appears in connection with the hyperbolic secant distribution.
Quickly converging series
The following two formulas involve quickly converging series, and are thus appropriate for numerical computation: |
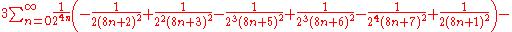 |
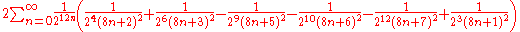 |
and
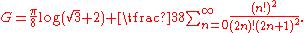
The theoretical foundations for such series is given by Broadhurst (the first formula) and Ramanujan (the second formula) The algorithms for fast evaluation of the Catalan constant is constructed by E. Karatsuba.
Known digits
The number of known digits of Catalan's constant G has increased dramatically during the last decades. This is due both to the increase of performance of computers as well as to algorithmic improvements.| Date | Decimal digits | Computation performed by |
|---|---|---|
| 1832 | 16 | Thomas Clausen Thomas Clausen (mathematician) Thomas Clausen was a Danish mathematician and astronomer.... |
| 1858 | 19 | Carl Johan Danielsson Hill |
| 1864 | 14 | Eugène Charles Catalan Eugène Charles Catalan Eugène Charles Catalan was a French and Belgian mathematician.- Biography :Catalan was born in Bruges , the only child of a French jeweller by the name of Joseph Catalan, in 1814. In 1825, he traveled to Paris and learned mathematics at École Polytechnique, where he met Joseph Liouville... |
| 1877 | 20 | James W. L. Glaisher James Whitbread Lee Glaisher James Whitbread Lee Glaisher son of James Glaisher, the meteorologist, was a prolific English mathematician.He was educated at St Paul's School and Trinity College, Cambridge, where he was second wrangler in 1871... |
| 1913 | 32 | James W. L. Glaisher James Whitbread Lee Glaisher James Whitbread Lee Glaisher son of James Glaisher, the meteorologist, was a prolific English mathematician.He was educated at St Paul's School and Trinity College, Cambridge, where he was second wrangler in 1871... |
| 1990 | 20,000 | Greg J. Fee |
| 1996 | 50,000 | Greg J. Fee |
| August 14, 1996 | 100,000 | Greg J. Fee & Simon Plouffe Simon Plouffe Simon Plouffe is a Quebec mathematician born on June 11, 1956 in Saint-Jovite, Quebec. He discovered the formula for the BBP algorithm which permits the computation of the nth binary digit of π, in 1995... |
| September 29, 1996 | 300,000 | Thomas Papanikolaou |
| 1996 | 1,500,000 | Thomas Papanikolaou |
| 1997 | 3,379,957 | Patrick Demichel |
| January 4, 1998 | 12,500,000 | Xavier Gourdon |
| 2001 | 100,000,500 | Xavier Gourdon & Pascal Sebah |
| 2002 | 201,000,000 | Xavier Gourdon & Pascal Sebah |
| October 2006 | 5,000,000,000 | Shigeru Kondo & Steve Pagliarulo |
| August 2008 | 10,000,000,000 | Shigeru Kondo & Steve Pagliarulo |
| January 31, 2009 | 15,510,000,000 | Alexander J. Yee & Raymond Chan |
| April 16, 2009 | 31,026,000,000 | Alexander J. Yee & Raymond Chan |

