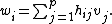Cartan's lemma
Encyclopedia
In mathematics
, Cartan's lemma refers to a number of results named after either Élie Cartan
or his son Henri Cartan
:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Cartan's lemma refers to a number of results named after either Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
or his son Henri Cartan
Henri Cartan
Henri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
:
- In exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
: Suppose that v1, ..., vp are linearly independent elements of a vector space V and w1, ..., wp are such that
-
- in ΛV. Then there are scalars hij = hji such that
- In several complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
: Let and and define rectangles in the complex plane C by
-

- so that
 . Let K2, ..., Kn be simply connected domains in C and let
. Let K2, ..., Kn be simply connected domains in C and let

- so that again
 . Suppose that F(z) is a complex analytic matrix-valued function on a rectangle K in Cn such that F(z) is an invertible matrix for each z in K. Then there exist analytic functions
. Suppose that F(z) is a complex analytic matrix-valued function on a rectangle K in Cn such that F(z) is an invertible matrix for each z in K. Then there exist analytic functions 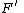 in
in  and
and 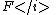 in
in  such that
such that
- in K.
- In potential theoryPotential theoryIn mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
, a result that estimates the Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
of the set on which a logarithmic Newtonian potentialNewtonian potentialIn mathematics, the Newtonian potential or Newton potential is an operator in vector calculus that acts as the inverse to the negative Laplacian, on functions that are smooth and decay rapidly enough at infinity. As such, it is a fundamental object of study in potential theory...
is small. See Cartan's lemma (potential theory)Cartan's lemma (potential theory)In potential theory, a branch of mathematics, Cartan's lemma, named after Henri Cartan, is a bound on the measure and complexity of the set on which a logarithmic Newtonian potential is small. The following statement can be found in Levin's book....
.
- so that again
- so that