
Calibrated geometry
Encyclopedia
In the mathematical
field of differential geometry, a calibrated manifold is a Riemannian manifold
(M,g) of dimension n equipped with a differential p-form
φ (for some 0 ≤ p ≤ n) which is a calibration in the sense that
Set Gx(φ) = { ξ as above : φ|ξ = volξ }. (In order for the theory to be nontrivial, we need Gx(φ) to be nonempty.) Let G(φ) be the union of Gx(φ) for x in M.
The theory of calibrations is due to R. Harvey and B. Lawson and others (see The History of Calibrations).
A famous one line argument shows that calibrated p-submanifolds minimize volume within their homology class. Indeed, suppose that Σ is calibrated, and Σ ′ is a p submanifold in the same homology class. Then
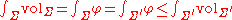
where the first equality holds because Σ is calibrated, the second equality is Stokes' theorem
(as φ is closed), and the third equality holds because φ is a calibration.
(1936), explicit for complex analytic submanifolds in Georges de Rham
[1] (1957), and applied to singular
complex varieties in the context of rectifiable currents by Herbert Federer
[3, §4]
(1965). Marcel Berger
[2, §6, last paragraph] (1970) was the first to extract the under-
lying principle and apply it to other examples such as quaternionic varieties,
followed by Dao (1977). The term calibration was coined in the landmark
paper of Harvey and Lawson, which discovered rich new calibrated geometries of “special Lagrangian,” “associative,” and “Cayley” varieties.
The method has grown in power and applications. Surveys appear in Morgan
[1, 2]. Mackenzie and Lawlor use calibrations in the proof (Nance; Lawlor
[1]) of the angle conjecture on when a pair of m-planes in Rn is area mini-
mizing. The “vanishing calibrations” of Lawlor [3] actually provide sufficient
differential-geometric conditions for area minimization, a classification of
all area-minimizing cones over products of m spheres, examples of nonori-
entable area-minimizing cones, and singularities stable under perturbations.
The “paired calibrations” of Lawlor and Morgan [2] and of Brakke [1, 2] and
the covering space calibrations of Brakke [3] prove new examples of soap
films in R3, in R4, and above. Other developments include Murdoch’s “twisted calibrations” of nonorientable surfaces, Le’s “relative calibrations” of stable surfaces, and Pontryagin calibrations on Grassmannians (Gluck, Mackenzie, and Morgan).
Lawlor [2] has developed a related theory for proving minimization by
slicing. Lawlor and Morgan [1] show, for example, that three minimal surfaces meeting at 120 degrees minimize area locally.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of differential geometry, a calibrated manifold is a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(M,g) of dimension n equipped with a differential p-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
φ (for some 0 ≤ p ≤ n) which is a calibration in the sense that
- φ is closed: dφ = 0, where d is the exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
- for any x ∈ M and any oriented p-dimensional subspace ξ of TxM, φ|ξ = λ volξ with λ ≤ 1. Here volξ is the volume form of ξ with respect to g.
Set Gx(φ) = { ξ as above : φ|ξ = volξ }. (In order for the theory to be nontrivial, we need Gx(φ) to be nonempty.) Let G(φ) be the union of Gx(φ) for x in M.
The theory of calibrations is due to R. Harvey and B. Lawson and others (see The History of Calibrations).
Calibrated submanifolds
A p-dimensional submanifold Σ of M is said to be a calibrated submanifold with respect to φ (or simply φ-calibrated) if TΣ lies in G(φ).A famous one line argument shows that calibrated p-submanifolds minimize volume within their homology class. Indeed, suppose that Σ is calibrated, and Σ ′ is a p submanifold in the same homology class. Then
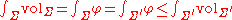
where the first equality holds because Σ is calibrated, the second equality is Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
(as φ is closed), and the third equality holds because φ is a calibration.
Examples
- On a Kähler manifoldKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, suitably normalized powers of the Kähler form are calibrations, and the calibrated submanifolds are the complex submanifolds. - On a Calabi-Yau manifoldCalabi-Yau manifoldA Calabi-Yau manifold is a special type of manifold that shows up in certain branches of mathematics such as algebraic geometry, as well as in theoretical physics...
, the real part of a holomorphic volume form (suitably normalized) is a calibration, and the calibrated submanifolds are special Lagrangian submanifolds. - On a G2-manifoldG2 manifoldIn differential geometry, a G2 manifold is a seven-dimensional Riemannian manifold with holonomy group G2. The group G_2 is one of the five exceptional simple Lie groups...
, both the 3-form and the Hodge dual 4-form define calibrations. The corresponding calibrated submanifolds are called associative and coassociative submanifolds. - On a Spin(7)-manifoldSpin(7)-manifoldIn mathematics, a Spin-manifold is an eight-dimensional Riemannian manifold with the exceptional holonomy group Spin. Spin-manifolds are Ricci-flat and admit a parallel spinor. They also admit a parallel 4-form, known as the Cayley form, which is a calibrating form for a special class of...
, the defining 4-form, known as the Cayley form, is a calibration. The corresponding calibrated submanifolds are called Cayley submanifolds.
History of Calibrations (Geometric Measure Theory, Chapter 6, Section 6.5, Frank Morgan)
The original example of complex analytic varieties was implicit in Wilhelm WirtingerWilhelm Wirtinger
Wilhelm Wirtinger was an Austrian mathematician, working in complex analysis, geometry, algebra, number theory, Lie groups and knot theory.-Biography:...
(1936), explicit for complex analytic submanifolds in Georges de Rham
Georges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
[1] (1957), and applied to singular
complex varieties in the context of rectifiable currents by Herbert Federer
Herbert Federer
Herbert Federer was an American mathematician. He is one of the creators of geometric measure theory, at the meeting point of differential geometry and mathematical analysis.-Career:...
[3, §4]
(1965). Marcel Berger
Marcel Berger
Marcel Berger is a French mathematician, doyen of French differential geometry, and a former director of the Institut des Hautes Études Scientifiques , France...
[2, §6, last paragraph] (1970) was the first to extract the under-
lying principle and apply it to other examples such as quaternionic varieties,
followed by Dao (1977). The term calibration was coined in the landmark
paper of Harvey and Lawson, which discovered rich new calibrated geometries of “special Lagrangian,” “associative,” and “Cayley” varieties.
The method has grown in power and applications. Surveys appear in Morgan
[1, 2]. Mackenzie and Lawlor use calibrations in the proof (Nance; Lawlor
[1]) of the angle conjecture on when a pair of m-planes in Rn is area mini-
mizing. The “vanishing calibrations” of Lawlor [3] actually provide sufficient
differential-geometric conditions for area minimization, a classification of
all area-minimizing cones over products of m spheres, examples of nonori-
entable area-minimizing cones, and singularities stable under perturbations.
The “paired calibrations” of Lawlor and Morgan [2] and of Brakke [1, 2] and
the covering space calibrations of Brakke [3] prove new examples of soap
films in R3, in R4, and above. Other developments include Murdoch’s “twisted calibrations” of nonorientable surfaces, Le’s “relative calibrations” of stable surfaces, and Pontryagin calibrations on Grassmannians (Gluck, Mackenzie, and Morgan).
Lawlor [2] has developed a related theory for proving minimization by
slicing. Lawlor and Morgan [1] show, for example, that three minimal surfaces meeting at 120 degrees minimize area locally.

