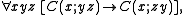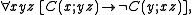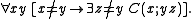C-minimal theory
Encyclopedia
In model theory
, a branch of mathematical logic
, a C-minimal theory is a theory that is "minimal" with respect to a ternary relation
C with certain properties. Algebraically closed fields with a (Krull) valuation are perhaps the most important example.
This notion was defined in analogy to the o-minimal theories
, which are "minimal" (in the same sense) with respect to a linear order.
A C-minimal structure is a structure
M, in a signature
containing the symbol C, such that C satisfies the above axioms and every set of elements of M that is definable with parameters in M is a Boolean combination of instances of C, i.e. of formulas of the form C(x;bc), where b and c are elements of M.
A theory is called C-minimal if all of its models are C-minimal. A structure is called strongly C-minimal if its theory is C-minimal. One can construct C-minimal structures which are not strongly C-minimal.
p and a p-adic number
a let |a|p denote its p-adic norm. Then the relation defined by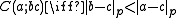 is a C-relation, and the theory of Qp is with addition and this relation is C-minimal. The theory of Qp as a field, however, is not C-minimal.
is a C-relation, and the theory of Qp is with addition and this relation is C-minimal. The theory of Qp as a field, however, is not C-minimal.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a C-minimal theory is a theory that is "minimal" with respect to a ternary relation
Triadic relation
In mathematics, a ternary relation or triadic relation is a finitary relation in which the number of places in the relation is three. Ternary relations may also be referred to as 3-adic, 3-ary, 3-dimensional, or 3-place....
C with certain properties. Algebraically closed fields with a (Krull) valuation are perhaps the most important example.
This notion was defined in analogy to the o-minimal theories
O-minimal theory
In mathematical logic, and more specifically in model theory, an infinite structure which is totally ordered by In mathematical logic, and more specifically in model theory, an infinite structure which is totally ordered by...
, which are "minimal" (in the same sense) with respect to a linear order.
Definition
A C-relation is a ternary relation C(x;yz) that satisfies the following axioms.A C-minimal structure is a structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
M, in a signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
containing the symbol C, such that C satisfies the above axioms and every set of elements of M that is definable with parameters in M is a Boolean combination of instances of C, i.e. of formulas of the form C(x;bc), where b and c are elements of M.
A theory is called C-minimal if all of its models are C-minimal. A structure is called strongly C-minimal if its theory is C-minimal. One can construct C-minimal structures which are not strongly C-minimal.
Example
For a prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p and a p-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
a let |a|p denote its p-adic norm. Then the relation defined by
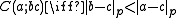 is a C-relation, and the theory of Qp is with addition and this relation is C-minimal. The theory of Qp as a field, however, is not C-minimal.
is a C-relation, and the theory of Qp is with addition and this relation is C-minimal. The theory of Qp as a field, however, is not C-minimal.