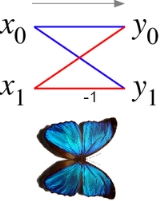
Butterfly diagram
Encyclopedia
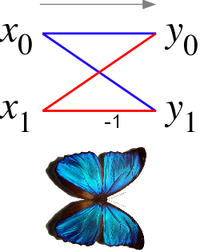
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
algorithms, a butterfly is a portion of the computation that combines the results of smaller discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
s (DFTs) into a larger DFT, or vice versa (breaking a larger DFT up into subtransforms). The name "butterfly" comes from the shape of the data-flow diagram in the radix-2 case, as described below. The same structure can also be found in the Viterbi algorithm
Viterbi algorithm
The Viterbi algorithm is a dynamic programming algorithm for finding the most likely sequence of hidden states – called the Viterbi path – that results in a sequence of observed events, especially in the context of Markov information sources, and more generally, hidden Markov models...
, used for finding the most likely sequence of hidden states.
Most commonly, the term "butterfly" appears in the context of the Cooley–Tukey FFT algorithm, which recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
breaks down a DFT of composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
size n = rm into r smaller transforms of size m where r is the "radix" of the transform. These smaller DFTs are then combined via size-r butterflies, which themselves are DFTs of size r (performed m times on corresponding outputs of the sub-transforms) pre-multiplied by roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
(known as twiddle factor
Twiddle factor
A twiddle factor, in fast Fourier transform algorithms, is any of the trigonometric constant coefficients that are multiplied by the data in the course of the algorithm...
s). (This is the "decimation in time" case; one can also perform the steps in reverse, known as "decimation in frequency", where the butterflies come first and are post-multiplied by twiddle factors. See also the Cooley–Tukey FFT article.)
Radix-2 butterfly diagram
In the case of the radix-2 Cooley–Tukey algorithm, the butterfly is simply a DFT of size-2 that takes two inputs (x0, x1) (corresponding outputs of the two sub-transforms) and gives two outputs (y0, y1) by the formula (not including twiddlefactors):
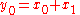
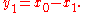
If one draws the data-flow diagram for this pair of operations, the (x0, x1) to (y0, y1) lines cross and resemble the wings of a butterfly
Butterfly
A butterfly is a mainly day-flying insect of the order Lepidoptera, which includes the butterflies and moths. Like other holometabolous insects, the butterfly's life cycle consists of four parts: egg, larva, pupa and adult. Most species are diurnal. Butterflies have large, often brightly coloured...
, hence the name (see also the illustration at right).
More specifically, a decimation-in-time FFT algorithm on n = 2 p inputs with respect to a primitive n-th root of unity ω = exp(2πi / n) relies on O(n log n) butterflies of the form:


where k is an integer depending on the part of the transform being computed. Whereas the corresponding inverse transform can mathematically be performed by replacing ω with ω−1 (and possibly multiplying by an overall scale factor, depending on the normalization convention), one may also directly invert the butterflies:
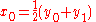
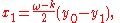
corresponding to a decimation-in-frequency FFT algorithm.

