
Brodal queue
Encyclopedia
In computer science
, the Brodal queue is a heap
/priority queue
structure with very low worst case
time bounds
: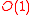 for insertion, find-minimum, meld (merge two queues) and decrease-key and
for insertion, find-minimum, meld (merge two queues) and decrease-key and 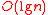 for delete-minimum and general deletion; they are the first heap variant with these bounds. Brodal queues are named after their inventor Gerth Stølting Brodal.
for delete-minimum and general deletion; they are the first heap variant with these bounds. Brodal queues are named after their inventor Gerth Stølting Brodal.
While having better asymptotic bounds than other priority queue structures, they are, in the words of Brodal himself, "quite complicated" and "[not] applicable in practice."
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the Brodal queue is a heap
Heap (data structure)
In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if B is a child node of A, then key ≥ key. This implies that an element with the greatest key is always in the root node, and so such a heap is sometimes called a max-heap...
/priority queue
Priority queue
A priority queue is an abstract data type in computer programming.It is exactly like a regular queue or stack data structure, but additionally, each element is associated with a "priority"....
structure with very low worst case
Best, worst and average case
In computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively...
time bounds
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
:
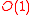 for insertion, find-minimum, meld (merge two queues) and decrease-key and
for insertion, find-minimum, meld (merge two queues) and decrease-key and 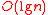 for delete-minimum and general deletion; they are the first heap variant with these bounds. Brodal queues are named after their inventor Gerth Stølting Brodal.
for delete-minimum and general deletion; they are the first heap variant with these bounds. Brodal queues are named after their inventor Gerth Stølting Brodal.While having better asymptotic bounds than other priority queue structures, they are, in the words of Brodal himself, "quite complicated" and "[not] applicable in practice."

