Bretschneider's formula
Encyclopedia
In geometry
, Bretschneider's formula is the following expression for the area
of a general convex quadrilateral
:
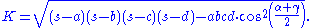
Here, a, b, c, d are the sides of the quadrilateral, s is the semiperimeter
, and
and 
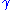are two opposite angles.
Bretschneider's formula works on any convex quadrilateral regardless of whether it is cyclic
or not.
The German mathematician Carl Anton Bretschneider
discovered the formula in 1842. The formula was also derived in the same year by the German mathematician Karl Georg Christian von Staudt
.
Therefore
The Law of Cosines
implies that
because both sides equal the square of the length of the diagonal BD. This can be rewritten as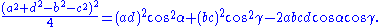
Substituting this in the above formula for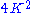
yields
This can be written as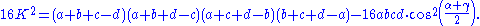
Introducing the semiperimeter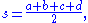
the above becomes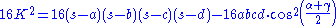
and Bretschneider's formula follows.
for the area of a cyclic quadrilateral
, which in turn generalizes Heron's formula for the area of a triangle
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Bretschneider's formula is the following expression for the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of a general convex quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
:
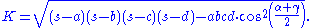
Here, a, b, c, d are the sides of the quadrilateral, s is the semiperimeter
Semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
, and
and 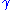are two opposite angles.Bretschneider's formula works on any convex quadrilateral regardless of whether it is cyclic
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
or not.
The German mathematician Carl Anton Bretschneider
Carl Anton Bretschneider
Carl Anton Bretschneider was a mathematician from Gotha, Germany. Bretschneider worked in geometry, number theory, and history of geometry. He also worked on logarithmic integrals and mathematical tables. He was one of the first mathematicians to use the symbol γ for Euler's constant when he...
discovered the formula in 1842. The formula was also derived in the same year by the German mathematician Karl Georg Christian von Staudt
Karl Georg Christian von Staudt
Karl Georg Christian von Staudt was a German mathematician born in the Free Imperial City of Rothenburg, which is now called Rothenburg ob der Tauber in Germany. From 1814 he studied in Gymnasium in Ausbach. He attended the University of Göttingen from 1818 to 1822 where he studied with Gauss who...
.
Proof of Bretschneider's formula
Denote the area of the quadrilateral by K. Then we haveTherefore
The Law of Cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
implies that
because both sides equal the square of the length of the diagonal BD. This can be rewritten as
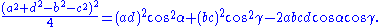
Substituting this in the above formula for
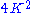yieldsThis can be written as
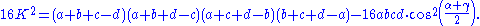
Introducing the semiperimeter
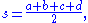
the above becomes
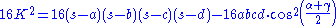
and Bretschneider's formula follows.
Related formulas
Bretschneider's formula generalizes Brahmagupta's formulaBrahmagupta's formula
In Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
for the area of a cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
, which in turn generalizes Heron's formula for the area of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
.